Mac用プロットライブラリ-16「シンプレックス法のアルゴリズム」

昼過ぎて日が出てきやがった。くそー。もう遅いわい。
前回、行列で表現した線形計画問題を、ふたつの行列に分解した。この効能について。

アルゴリズムの第1段階

まえやった変形が役に立つところ。前回作った式-25の小行列Bは正方のM×M行列で、xをM次元のベクトルとして、この小行列に関する方程式

はかならず解を持つ。この解をxBとする。このベクトルとすべての要素が0のxVを使えば式27を満たす。つまり

とすれば第2項は0なので成り立つ。ということは、xBの要素をM番目までもってそれ以降は0のN次元のベクトルxB

は

を当然満たす。ただし、この解が要素全部が非負であると言う条件を満たすとは限らない。また、非負であったとしても最適解であるとは限らない。のだけど、

もし条件を満たしたものがあったなら

ここでもしたまたまラッキーなことにxBの要素がすべて非負だったとする。ただし、最適解かどうかはわからないとする。
このとき評価関数zBは

である。

分解された行列に対する問題の両辺にB^-1を左からかけると

となる。ここで

と書いた。
式-27から

とすれば、式-11を満たす。従って分解した評価関数に上式を代入して

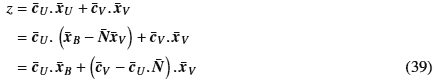
ということは、もし

の（これはN-M次元ベクトル）j番目の要素が負だったとするとxVのj番目の要素を大きくすると評価関数の値をここからさらに小さくできる、ということになる。

もし、要素の符号が全部正だったとすると、これ以上評価関数の値を小さくすることはできないので最初にあった解xBが最適解だった、ということになる。

じゃあ、xVのj番目の要素をどこまで大きくできるか、というと式-38からNのj番目の列ベクトルをN^jとすると、

の中の最小のものとなる。つまりここまでならxUのすべての成分を非負に保つことができる。

これをやると、最初全部の要素が0だったxVのj番目の要素を0で無くする代わりにxBのi番目の要素を0にする、という入れ替えをすることになる。従って式-40の負の要素に対応する変数を、ほかの変数が0になるまで0から大きくしていけばいい、ということになる。

もし、式-41の最小の値が負だったとすると、解の要素を0にすることなく評価関数の値をいくらでも小さくできるということになる。そんな問題、解くまでもなかろ。

そとあと

式-40の要素でまだ負の要素があったとすると、もう一度やればいいような気がするけど、そうすると、さっき0にした、xBのi番目の要素はこんどは0でなくなる。つまりxUの要素の0の数は増えないのに、xVの0の数は減ってしまう。それはもとのn変数で考えると、頂点ではなくなってしまう。頂点をたどるためには、つねに少なくともN-M個の要素は0でなければならない。

ということで面倒なんだけど、Bのi番目の行ベクトルと、Nのj番目の行ベクトルを入れ替え、それに対してもう一度式-31を解き直さなければいけない。そこから同じことを繰り返して、より小さな評価関数を目指す。小さくできなくなったらおしまいで、それが最適解ということになる。

う～ん、あまり慣れてないので難しい。