Zernike多項式 - その2 Zernike多項式とは

急に思い出して始めたZernike多項式のメモ。懐かしい。案外覚えているもんだわ。昔の話は忘れないというのはジジイの証拠。まあええとして。

直交関数系としてのZernike多項式

Zerike 多項式U_n^m(ρ,θ)は座標原点を中心にする単位円（半径1の円）の内部で定義された関数で

というようなものでR_n^m(ρ)は動径多項式と呼ばれるものである。mの正負の区別は便宜上のもので、Fourier級数をe^{i nθ}で書いたりcos nθとsin nθで書いたりするのと同じことである。

もともと丸いレンズの瞳の中で連続な収差を表現するために作られたので、丸いもののなかに連続に分布する「なにか」を表現するのに便利になっている。

図-1にZernike多項式の例を示す。ちなみにこれは式-4の(n,m)=(5,1)の場合の多項式の値をz方向に示している。単位円の外は値を持たないけど表示のために便宜的にz=0としてある。

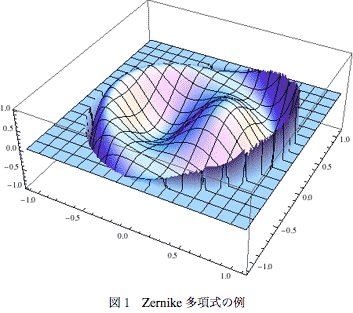
具体的な多項式の形はあとで説明するが、Mathematica6.0以降が手元にあればZernikeRを評価することで見ることができる。

直交関数系なので単位円内で定義された任意の関数W(ρ,θ)を

として近似することができる。その係数のα_n,mはFourier展開と全く同じで

で求めることができる。これは式-5を式-6の右辺に代入して、直交性を使うことで証明できる。

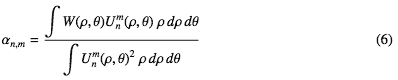
ちなみに、もしU_n^m(ρ,θ)が正規性を持っていたとしたら、式-6の分母は1になって簡単になる。これが正規性の利点。今となってはたいしたことないけど、式を手で書いていた時代はありがたかった。

と、ここまでが前置き。次は添字がnとmの2個あるけど、それを1列に並べましょう、という話。