Zernike多項式 - その8 使用例その2

前回、比較的簡単な単位円内の回転対称な関数をZernike多項式を使って展開した。もうひとつのちょっとだけ違った例。と、また例によって限界について。

もうひとつの例

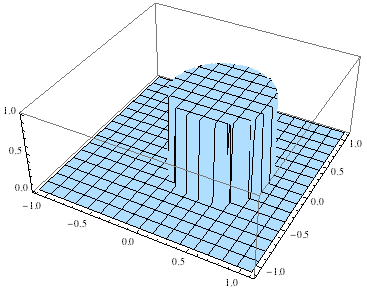
さて、ではもうひとつの例として同じ円筒型で中心位置をずらしたもの

1. (1/4,0)の位置を中心として半径1/2の内部は1
2. その外は0

でやってみる。

これは回転対称にはならないけどy方向には対称になっている。同じように80個までで係数を計算すると、

In[78]:= coef2=Table[
    (Integrate[zernikeCartesianPolynomial[p][x, y],
　　　　　　 {x, -1/4, 3/4}, {y, 0, Sqrt[1/4 - (x - 1/4)^2]}]
    + Integrate[zernikeCartesianPolynomial[p][x, y],
　　　　　　 {x, -1/4, 3/4}, {y, -Sqrt[1/4 - (x - 1/4)^2], 0}])
       /(Pi/rmsCoefficient[p]^2), {p, 0, 80}]

Out[78]= {1/4, 1/4, 0, -(15/32), 3/32, 0, -(17/32),
  0, 135/512, 1/32, 0, -(25/128), 0, 147/512, 0, -(175/4096),
  5/512, 0, -(57/1024), 0, 217/8192, 0, 651/4096, 0,
  6075/131072, 3/1024, 0, -(49/4096), 0, -(199/4096),
  0, 4383/16384, 0, -(31245/131072), 0, -(79673/1048576),
  7/8192, 0, -(5/4096), 0, -(1377/32768), 0, 12925/65536, 0,
  -(285197/1048576), 0, 77601/1048576, 0, -(208845/16777216),
  1/4096, 0, 9/16384, 0, -(1495/65536), 0, 26191/262144, 0,
  -(141801/1048576), 0, 77909/4194304, 0, -(1104089/16777216),
   0, 10481505/134217728, 9/131072, 0, 125/262144, 0,
   -(20977/2097152), 0, 80895/2097152, 0, -(776477/33554432), 0,
   -(7321727/67108864), 0, 55087125/536870912, 0, 18670387/134217728,
   0, -(347065965/8589934592)}

半分近くが0になってるけど、これはy方向に非対称な式（のはず）。

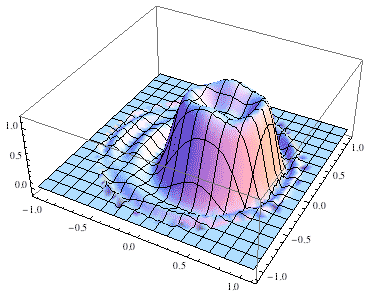
おなじようにプロットしてみる

Plot3D[
  Evaluate[Expand[Table[
      zernikeCartesianPolynomial[p][x, y], {p, 0, 80}].coef2]*circle[x, y]],
             {x, -1.1, 1.1}, {y, -1.1, 1.1}]

と

のようになる。 中心が原点にあったときに較べて展開精度は悪そうに見える。

Zernike多項式と現実のレンズ

これはZernike多項式の特徴で、回転対称性の低い関数の展開は苦手。もとはと言えば座標を回転させても形式が変わらないという制約から来ている。

顕微鏡対物などの回折限界レンズの設計の現場などではZernike多項式はよく使われて、性能評価に役立っているけど、そのレンズを作る現場では、一筋縄でいかないことが多い。

その原因のひとつには、組み立てた現物のレンズには対称軸なんて存在しない、ということがある。機械的に位置決めした絞りがレンズに対して横ずれするということはよくあって、これはさきほど例に見た円筒関数の横ずらしと同じことが起こる。

つまり、絞りの位置がずれる（中心が原点にない）だけで、波面収差をZernike展開すると非対称な高次の項がぞろぞろ出てくることになる。

そういったこと以外にも、例えば反射望遠鏡のようなドーナッツ型（真ん中に穴があいている）の波面収差や、高画角のレンズでビグネッティング（光のレンズ枠によるケラレ）が起こって楕円形になった瞳などのZernike展開では、ちょとした測定誤差のせいで展開係数が全く変わってしまったりすることがある。

これはZernike多項式が単位円の内部で直交していて、定義域をドーナッツ型や楕円形にすると直交関数系にならないからという単純な事実のためである。

本当なら瞳の形によって直交関数系を組み立て直せばいいのだけど、その場合、一般論を組み立てるのが難しくなる。例えばドーナッツ型の内部で直交する関数列は穴の半径に対する比率が違えば違った関数列になってしまう。

Zernike多項式は回折限界の光学系の評価には非常に有力な道具である。でも、何でもそうだけどやはり限界があってその限界を頭に置いて使う必要がある。