つづき。前回波動方程式を導出した。その解を、Fourier展開で形式的に求めてみる。徐々に疑問の核心に近づいて行く。
解のFourier展開
この式-33の一般解を書くためにEをFourier展開する。
ε(
k,ω)は展開係数である。ここで
aは
で実の場から展開係数を積分で表したときにつじつまを合わせるための定数で、この場合非対称(Fourier変換と逆変換で)になるけど途中で2πが現れなくてすむ。この定数がうるさいので
とする流儀もある。Fourier変換/逆変換を行ったり来たりする人にはこっちの方が便利だけど、こんどは
eの肩にいつも2πがつく。
このままでは紛らわしいので、場所と時間の場の量であることを強調するためにもとの電場をいちいちE(x,t)と書くことにする。
E(x,t)は実数の場なのですくなくとも
となっている必要がある。ここで
A†は
Aの複素共役である。
式-34を式-33に代入して、Fourier展開の性質
や
などを使うと
となる。ここで
のことで、また
である。これはεとμの時間に関するFourier展開となっている。
これらも当然、場の量と同じようにもとのτに関する量が実数なので、すくなくとも
のはずである。
式-39から、境界条件なり初期条件を満たしたうえで
を満足するような展開ができれば、それは自動的に式-33を満たすことになり、固有の問題の解が決まるということになる。
この式-45の条件をkとωに対する制約とみて
を分散関係(dispersion relation)と呼ぶ。式-46は等方な空間を仮定したのでベクトル
kの向きにはよらず、大きさだけを決める式になっている。
ここで
と書くと、
kとωは実数なので
となって、たまたまこれがうまいぐあいに満たされるような媒質でなければ解はない。解が無い場合は、場をFourier展開することはできないという結果になる。これは普通はその媒質では平面波は伝播しない、というふうに表現される。
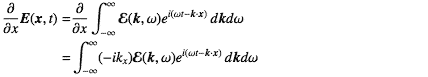
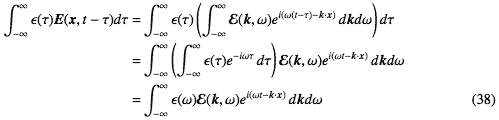



コメント 0