考え中 - Fourier領域と実領域の光（9）

前回までで平面波というのはFourier展開した項をひとつ取り出したものだ、ということを示した。では、いつでもそう言えるのか？

平面波が解にならない例として、導電率が0でない場合のMaxwellの方程式を考えてみる。

電信方程式の導出

物質方程式の中身に突っ込む前に、波動方程式を導いたときとは違う条件でMaxwellの方程式を変形してみる。

式-22以降では式-21、つまり電流は流れることはできないとした。次に真電荷はないが電流は流れ得る

としてみると、

となる。ただしここでもやはりεなどと同じようにσは一様だが因果律に従う量だとした。例えば金属の内部のような場を表していると考えられる。

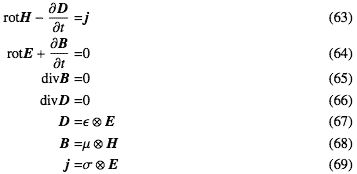
式-67から69を式-63と64に代入すると

波動方程式を導いたときと同じように式-70の時間微分をとってμと畳み込みして式-71のrotをとったものと辺々引き算すしてHを消去すると

となる。まえの波動方程式と違って場の1階微分の項が残る。これを電信方程式と呼ぶ人がいる。

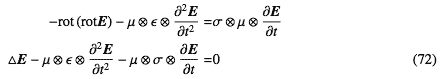
解のFourier展開に関する問題

波動方程式の場合と同じように式-34のFourier展開したEを式-72に代入して同じように整理すると

となる。ここで

である。 これは

を満たすようにkとωを調整すればいいように見えるが、これには解がない。なぜなら式の中にあらわに虚数単位iが含まれていて、特別な場合たとえばσ(ω)が実数部を持たない場合など以外では、実の量であるkとωでは満足させることができない。

従って式-62の場合のMaxwellの方程式の解は、式-34の形ではFourier展開できない、別の言い方をすればこの媒質内では平面波は伝播しない、ということになる。

ニュートンの運動方程式でも、時間に関する1階微分の項は摩擦などの損失を表していた。有限の値を持つσの場合、その元になる現象も実はエネルギーの散逸を伴っている。従って真空中の波動方程式の場合のように無限にどこまでも伝播する解が存在しないのは、あたりまえだろう。

もちろんFourier展開そのものは積分が実行可能ならできるので、遠くの方や未来で0になるような関数ももちろんFourier展開できる。しかしその場合に元の方程式とその境界条件を満足した上で展開できるかどうかはまた別問題。