小数展開をMIDIで演奏 - その3 [音楽の周辺]
先日、実数のB進数展開の桁の数字をそれぞれ音高に変換するというのをやった。有理数の場合、循環小数になるので短いフレーズが繰り返されるミニマルなメロディになる、ということを示した。
その最後に、長さL、音高の種類Bで完全にランダムな場合と違いがあるのか、という疑問を持った。ようするに有理数のB進数展開に、長さL音高の種類Bのすべての組み合わせが出現するか、と言う疑問。よく考えたら簡単だった。
ここの「循環小数が表す有理数」のところを見れば、具体的にその有理数を構成できる。ここでは10進数の場合で説明されているが一般のB進数の場合に拡張することは簡単にできる。つまり、ある有理数R(0 < R < 1)のB進数展開が循環小数になったとする。循環節の小数点以下n桁目の数字がan(1 ≤ n ≤ L)だとする。Rは となることがわかる。
ということはB−1以下の任意の数字をL個並べたものを循環節とするB進小数展開となるような有理数Rが作れる、ということになる。すなわち完全にランダムな場合と同じ循環節の組み合わせがあり得ることになる。
となることがわかる。
ということはB−1以下の任意の数字をL個並べたものを循環節とするB進小数展開となるような有理数Rが作れる、ということになる。すなわち完全にランダムな場合と同じ循環節の組み合わせがあり得ることになる。
具体的にMathematicaで作ってみると
例えば、前回やった1/7は十進展開すると0.142857142857142...だったが
ということはたとえばこの有理数
もっといけば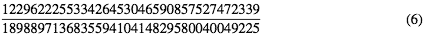 はこのような循環節のフレーズを持つことになる。知らない人のために説明しておくと、これはマイク・オールドフィールドというイギリス人が作った「Tubular Bells」という曲の冒頭で最も多く繰り返されるミニマルフレーズである。このミニマルな繰り返しがひとつの有理数で表されるということになる。
はこのような循環節のフレーズを持つことになる。知らない人のために説明しておくと、これはマイク・オールドフィールドというイギリス人が作った「Tubular Bells」という曲の冒頭で最も多く繰り返されるミニマルフレーズである。このミニマルな繰り返しがひとつの有理数で表されるということになる。
ということで、音高の任意の並びはどんな長さのどんな音程であれ、ひとつの有理数に対応させることができた。
このやりかたでは音の長さを指定することはできないけど、やりかたはいろいろ考えられる。ようするにエンコードの方法を考えればいい、ということにすぎない。また、和音も同じようにうまいエンコードを思いつけるか、という問題でしかない。さらに音色も同じである。一番手っ取り早い考え方はGeneral MIDIのデータ列を使えばいい。そうすると長い交響曲、例えばマーラーの第9番の交響曲もたったひとつの有理数で表すことができる、ということになる。
これはひとつの実数を指定するためには無限の情報量が必要になることに対応している。
面白い、というか不遜、というか。
その最後に、長さL、音高の種類Bで完全にランダムな場合と違いがあるのか、という疑問を持った。ようするに有理数のB進数展開に、長さL音高の種類Bのすべての組み合わせが出現するか、と言う疑問。よく考えたら簡単だった。
8 任意の進数の任意の循環節を持つ有理数
任意進数で任意の循環節を持つ有理数が作れる。ここの「循環小数が表す有理数」のところを見れば、具体的にその有理数を構成できる。ここでは10進数の場合で説明されているが一般のB進数の場合に拡張することは簡単にできる。つまり、ある有理数R(0 < R < 1)のB進数展開が循環小数になったとする。循環節の小数点以下n桁目の数字がan(1 ≤ n ≤ L)だとする。Rは

具体的にMathematicaで作ってみると
repeatingDecimal[peri_List, base_: 10] := Module[{np},
np = decimalSequence[peri, base];
np/(base^Length[peri] - 1)
]
decimalSequence[peri_List, base_] :=
With[{len = Length[peri]},
Sum[peri[[i]] base^(len - i), {i, len}]]
というようなrepeatingDecimalと言う関数を作る。これはふたつ目の引数の進数で循環節の数字のリストを与えるとその有理数を返す関数。例えば、前回やった1/7は十進展開すると0.142857142857142...だったが
In[15]:= repeatingDecimal[{1, 4, 2, 8, 5, 7}]
Out[15]= 1/7
となる。もっと一般的に
In[20]:= repeatingDecimal[{1, 2, 3, 4}, 5]
Out[20]= 97/312
In[21]:= RealDigits[%, 5]
Out[21]= {{{1, 2, 3, 4}}, 0}
などとなる(教えてもらったRealDigits関数を、さっそくうれしそうに使っている)。ということはたとえばこの有理数
In[59]:= r = repeatingDecimal[{1, 3, 5, 8, 10, 5, 8, 10}, 11]
Out[59]= 2573825/21435888
は
In[60]:= Sound[fractionalNotes[r, 16, digitBase -> 11, showDigits -> True]] Digit String = 1358a58a1358a58aとして音として鳴らせばこうなる。言うまでもないけど、つまり2573825/21435888というひとつの有理数はバッハの平均率1巻のハ長調のプレリュードの最初の小節の音の並びを表すことになる。
もっといけば
In[74]:= tubularBells = repeatingDecimal[
{5, 10, 5, 12, 5, 8, 10, 5, 13, 5, 15, 5, 12, 13, 5,
10, 5, 12, 5, 8, 10, 5, 13, 5, 15, 5, 12, 13, 5, 12}, 16]
Out[74]= 122962225533426453046590857527472339/189889713683559410414829580040049225
In[76]:= Sound[
fractionalNotes[tubularBells, 32, digitBase -> 16,
noteScale -> chromaticScale, showDigits -> True]]
Digit String = a5c58a5d5f5cd5a5c58a5d5f5cd5c5a5
とするとこの有理数
ということで、音高の任意の並びはどんな長さのどんな音程であれ、ひとつの有理数に対応させることができた。
このやりかたでは音の長さを指定することはできないけど、やりかたはいろいろ考えられる。ようするにエンコードの方法を考えればいい、ということにすぎない。また、和音も同じようにうまいエンコードを思いつけるか、という問題でしかない。さらに音色も同じである。一番手っ取り早い考え方はGeneral MIDIのデータ列を使えばいい。そうすると長い交響曲、例えばマーラーの第9番の交響曲もたったひとつの有理数で表すことができる、ということになる。
これはひとつの実数を指定するためには無限の情報量が必要になることに対応している。
面白い、というか不遜、というか。
2010-08-03 23:48
nice!(0)
コメント(0)
トラックバック(0)


コメント 0