最小2乗法 - その4 [最小2乗法のイメージ]
せっかく行列を考えたんだからすこし違う方向から見ていることにする。式-8をもういちど考える。
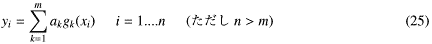 これは不能の方程式だった...
これは不能の方程式だった...
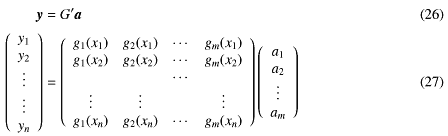 となる。この行列G′はn > mなので縦長の行列になっている。この代数的な構造を考えてみる。
となる。この行列G′はn > mなので縦長の行列になっている。この代数的な構造を考えてみる。
図-1のように、このG′はm次元ベクトル空間Rmからn次元ベクトル空間Rnへの写像と見ることができる。像空間IはG′の列ベクトルの張る空間である。何度も書くけどn > mなのでG′の列ベクトルがすべて独立だったとしても像空間はRn全体を張ることはできない。つまり像空間はRnの真部分空間になる。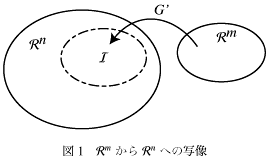 もし、yが像空間Iの中にあれば解があるが、必ずしもそうではない。従って一般的には条件が多すぎるので解はない、ということになる。
もし、yが像空間Iの中にあれば解があるが、必ずしもそうではない。従って一般的には条件が多すぎるので解はない、ということになる。
これをもう少しわかりやすくするために、例としてn=3、m=2の場合を考えてみる。その場合G′は3行2列の行列で、R2からR3への写像になる。
図-2のようにyは3次元空間内にある。いっぽう像空間Iは平面になる。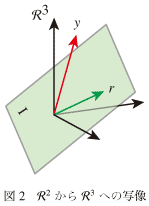 G′aは図中のrのようにI内にしかない。そして一般的にはyはI内にはないので、aをどのようにとったとしてもG′aをyと一致させることはできない。つまり解はない。
G′aは図中のrのようにI内にしかない。そして一般的にはyはI内にはないので、aをどのようにとったとしてもG′aをyと一致させることはできない。つまり解はない。
では、一歩さがって図-3のようなI内でyにもっとも近いベクトルを探すことにしよう。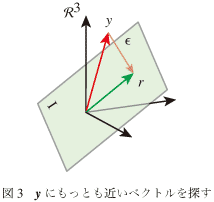 この「もっとも近い」というのは図中のϵが最も短くなるrを次善の解としよう、ということである。
この「もっとも近い」というのは図中のϵが最も短くなるrを次善の解としよう、ということである。
式-26からこのϵは である。
である。
これが一番短くなるのは、長さを計算するまでもなく、Iと直交する、つまりrとの内積が0になる場合である。すなわち ベクトルの内積は行列の積と同じスタイルで書くと
ベクトルの内積は行列の積と同じスタイルで書くと
 なのでこれで書き換えて整理すると
なのでこれで書き換えて整理すると
 この式は両辺スカラなので方程式としては数が足りない。しかし、aが0ベクトルでは意味がない(解ではない)ので
この式は両辺スカラなので方程式としては数が足りない。しかし、aが0ベクトルでは意味がない(解ではない)ので
 である必要がある。これは式だけ見てるとわからないけど両辺m個の要素のベクトルである。つまりこれだと式と変数の数が一致している。もうすこし書き換えると
である必要がある。これは式だけ見てるとわからないけど両辺m個の要素のベクトルである。つまりこれだと式と変数の数が一致している。もうすこし書き換えると
 となる。行列で書いてあるけど、G′は式-27にある通り
となる。行列で書いてあるけど、G′は式-27にある通り
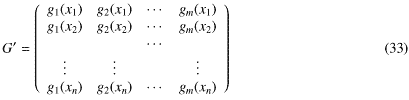 だった。
だった。
従って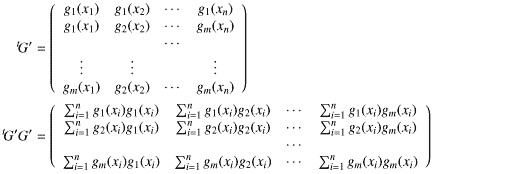 だから、式-32を要素で書くと
だから、式-32を要素で書くと
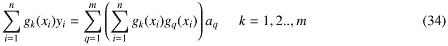 となる。ということは式-32は式-13とまったく同じ、ということになる。ちなみに式-32の形のほうを正規方程式と呼ぶこともある(中身は同じだけど)。
となる。ということは式-32は式-13とまったく同じ、ということになる。ちなみに式-32の形のほうを正規方程式と呼ぶこともある(中身は同じだけど)。
つまりどういうことかというと、誤差の2乗和を最小にするという条件は、条件過剰の方程式系に対して実現可能なものの中でもっとも「近い」ものを選ぶのと同じになる、ということである。これはもとはといえばベクトルの長さをユークリッドノルムで測る、ということに起因している。
この辺のことを良く知ってる人にとってはこのこと、つまり残差の2乗和を最小にすることと、代数的に近いベクトルを解とすることが一致するのはごく当たり前のことである。しかし、僕はその昔この事実に気がついたとき、代数のイメージは面白いと思った。
4 代数的な考え方
式-8(すなわち式-25)を行列で書いてみると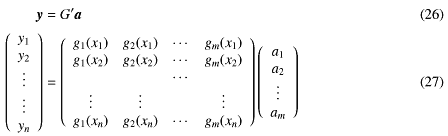
図-1のように、このG′はm次元ベクトル空間Rmからn次元ベクトル空間Rnへの写像と見ることができる。像空間IはG′の列ベクトルの張る空間である。何度も書くけどn > mなのでG′の列ベクトルがすべて独立だったとしても像空間はRn全体を張ることはできない。つまり像空間はRnの真部分空間になる。

これをもう少しわかりやすくするために、例としてn=3、m=2の場合を考えてみる。その場合G′は3行2列の行列で、R2からR3への写像になる。
図-2のようにyは3次元空間内にある。いっぽう像空間Iは平面になる。

では、一歩さがって図-3のようなI内でyにもっとも近いベクトルを探すことにしよう。

式-26からこのϵは
これが一番短くなるのは、長さを計算するまでもなく、Iと直交する、つまりrとの内積が0になる場合である。すなわち
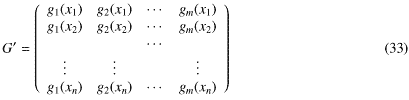
従って
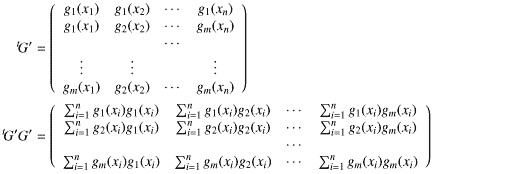
つまりどういうことかというと、誤差の2乗和を最小にするという条件は、条件過剰の方程式系に対して実現可能なものの中でもっとも「近い」ものを選ぶのと同じになる、ということである。これはもとはといえばベクトルの長さをユークリッドノルムで測る、ということに起因している。
この辺のことを良く知ってる人にとってはこのこと、つまり残差の2乗和を最小にすることと、代数的に近いベクトルを解とすることが一致するのはごく当たり前のことである。しかし、僕はその昔この事実に気がついたとき、代数のイメージは面白いと思った。
2013-11-23 21:27
nice!(0)
コメント(0)
トラックバック(0)


コメント 0