最小2乗法 - その8 [最小2乗法のイメージ]
ずいぶん間があいてしまった。前回までにGivens回転を使ったQR分解をやったので、もうあとほんの少しだけ残っている。完全に忘れないうちにやってしまおう。
追記:(2/23)
符号間違ってた。修正。
直交行列には回転以外にも鏡映という操作もある(操作そのものとしては独立ではないけど。例えば鏡映の組み合わせで任意の回転は表現できることは直感的にもわかる。ついでに言えば逆は成り立たない。つまり回転の組み合わせでは鏡映を表すことはできない)。もちろんこれを使ってもQR分解は可能である。この方法をHouseholder変換によるQR分解と言う。
Householder変換はHouseholder行列Hで表される。HはWikipediaによると であるという(転置の記号はこれまでのとあわせた)。ここでuは任意のベクトルで、Iは単位行列である。なんだかへんな形でこれだけではよくわからない。しかし、普通のベクトルxにこのHをかけてみると
であるという(転置の記号はこれまでのとあわせた)。ここでuは任意のベクトルで、Iは単位行列である。なんだかへんな形でこれだけではよくわからない。しかし、普通のベクトルxにこのHをかけてみると
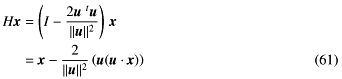 となる。tux = u·xでスカラになるので、もうちょっと読みやすいように書きなおすと
となる。tux = u·xでスカラになるので、もうちょっと読みやすいように書きなおすと
 で(大きなカッコの中はスカラ)、ここで∧u = u/||u||という規格化されたベクトルだとすると、書くまでもなく
で(大きなカッコの中はスカラ)、ここで∧u = u/||u||という規格化されたベクトルだとすると、書くまでもなく
 となって、これは3次元の場合では、図-14に示すようにずっと昔やった反射の式-47と全く同じである。
となって、これは3次元の場合では、図-14に示すようにずっと昔やった反射の式-47と全く同じである。
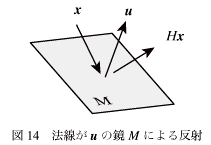 n次元の場合はn−1次元超平面での反射、ということになる。全然イメージがわかなくなるけど。
n次元の場合はn−1次元超平面での反射、ということになる。全然イメージがわかなくなるけど。
つまりHouseholder行列をかけるということは(列)ベクトルを、法線がuを向いた面で反射させる、ということと同じ、つまり鏡映をとるということに等しい。これをベクトル間の演算ではなく、行列の形で書いたのが式-60のHouseholder行列である、ということがわかる。
一般の行列Gの第1列の第1要素以外を0にすることを考える。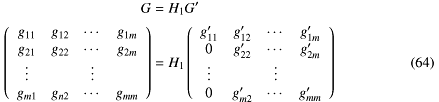 Gの第1列ベクトルg1をG′の第1列ベクトルg′1に鏡映で変換できればいい。これは式-60を
Gの第1列ベクトルg1をG′の第1列ベクトルg′1に鏡映で変換できればいい。これは式-60を
 とすればいいことは、もう図を書くのが面倒なのでやめるけど、3次元の場合のミラーによる反射を想像してみればすぐわかる。g′1の第1要素以外は0にしたいのだから、
とすればいいことは、もう図を書くのが面倒なのでやめるけど、3次元の場合のミラーによる反射を想像してみればすぐわかる。g′1の第1要素以外は0にしたいのだから、
 なので
なので
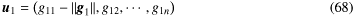 と簡単になる。
と簡単になる。
よく考えればこれだけではなくもうひとつ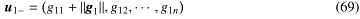 も、式-64の形になることがわかる。このときg′11の符号がさっきとは逆になる。
とりあえずは好きなほうを選べばいいけど、式-60には||u||が分母にくるので、このノルムが大きくなるほうを選ぶのが数値的には安全である(g11と同符号を選べばいいが、なんども言うように数値的な安定性が悪化しないだけであって、改善されるわけではない)。
も、式-64の形になることがわかる。このときg′11の符号がさっきとは逆になる。
とりあえずは好きなほうを選べばいいけど、式-60には||u||が分母にくるので、このノルムが大きくなるほうを選ぶのが数値的には安全である(g11と同符号を選べばいいが、なんども言うように数値的な安定性が悪化しないだけであって、改善されるわけではない)。
追記:(2/23)
符号間違ってた。修正。
3.3 Householder変換
もうずいぶん前になるけど、前回やったGivens回転によるQR分解は、回転だけを使って実行した。ある平面内での回転操作は直交行列になり、その積も直交行列なので、回転を使って上三角行列にできればそれはQR分解したことになる。直交行列には回転以外にも鏡映という操作もある(操作そのものとしては独立ではないけど。例えば鏡映の組み合わせで任意の回転は表現できることは直感的にもわかる。ついでに言えば逆は成り立たない。つまり回転の組み合わせでは鏡映を表すことはできない)。もちろんこれを使ってもQR分解は可能である。この方法をHouseholder変換によるQR分解と言う。
Householder変換はHouseholder行列Hで表される。HはWikipediaによると
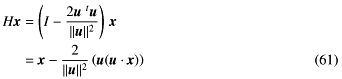

つまりHouseholder行列をかけるということは(列)ベクトルを、法線がuを向いた面で反射させる、ということと同じ、つまり鏡映をとるということに等しい。これをベクトル間の演算ではなく、行列の形で書いたのが式-60のHouseholder行列である、ということがわかる。
3.4 Householder行列によるQR分解
このHouseholder行列を使ったQR分解は、さっきのGivens回転でネタバレのようなものだけど、簡単にやってみる。一般の行列Gの第1列の第1要素以外を0にすることを考える。
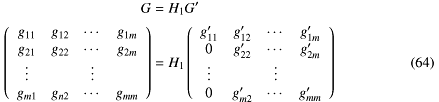
よく考えればこれだけではなくもうひとつ
2014-02-22 21:18
nice!(0)
コメント(0)
トラックバック(0)


コメント 0