最小2乗法 - その10 [最小2乗法のイメージ]
地道に続ける。前回でHouseholder変換を使って最小2乗法の正規方程式を、数値的安定性を壊さずに解く方法をまとめた。今回は縦に長い行列(もちろんqueueじゃなくてmatrixの話)による一次方程式から出発して最小2乗解を得る、という話。僕はこれが面白いと思うんだけど、ほかの人はどうだろう....
 と書いたので、Qの転置を計算しないといけないような気がするけど、実はこれは式を簡単にするためにこう書いただけで、転置を計算する必要はない。それは第k列を対象にしたHouseholder行列をHkと書くと
と書いたので、Qの転置を計算しないといけないような気がするけど、実はこれは式を簡単にするためにこう書いただけで、転置を計算する必要はない。それは第k列を対象にしたHouseholder行列をHkと書くと
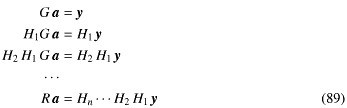 というふうにyに対してGの列ベクトルと同じことをすればいい。もちろんHouseholder行列の場合だけでなくGivens回転や、それ以外の行列を使ってQR分解するときでも同じである。これはQR分解を得るアルゴリズムから考えればあたりまえだし、代数的に考えても行列の列ベクトルと非斉次項のベクトルは同じ空間にあって、同じ操作を受けなければならないので、当然と言える。このおかげで計算は簡単になる。
というふうにyに対してGの列ベクトルと同じことをすればいい。もちろんHouseholder行列の場合だけでなくGivens回転や、それ以外の行列を使ってQR分解するときでも同じである。これはQR分解を得るアルゴリズムから考えればあたりまえだし、代数的に考えても行列の列ベクトルと非斉次項のベクトルは同じ空間にあって、同じ操作を受けなければならないので、当然と言える。このおかげで計算は簡単になる。
ここではちょっと見方を変えて、式-26(昔のここにある)の不能の方程式から出発してみる。もう一度書いてみると、n > mのときに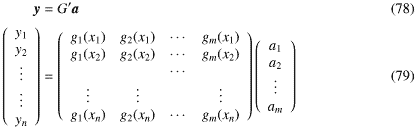 この行列G′はRmからRnへの写像と考えることができた。G′による像空間IはRn内のm次元の真部分空間になっている。
この行列G′はRmからRnへの写像と考えることができた。G′による像空間IはRn内のm次元の真部分空間になっている。
この部分空間Rmを、n次元の直交行列QをかけてRnのなかのn−m個の軸の成分を0にすることを考える。つまり3次元空間内の2次元空間の場合では図-16のような変換をするということである。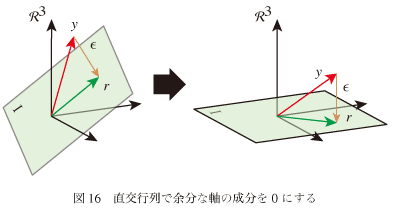 こういうのってなんて言うんだったっけ?
こういうのってなんて言うんだったっけ?
これができれば、式-79は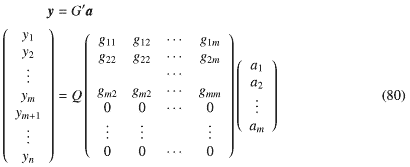 となって、両辺にtQをかけると
となって、両辺にtQをかけると
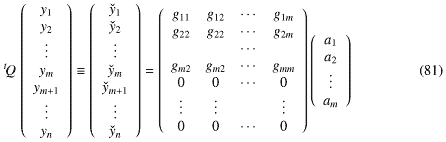 となる。不能の方程式であることはもちろんおなじだけど、最小2乗解はまえやったときと同じように図中のϵが最短となる場合であることにかわりはない。
となる。不能の方程式であることはもちろんおなじだけど、最小2乗解はまえやったときと同じように図中のϵが最短となる場合であることにかわりはない。
 と書くと、あきらかに式-81は
と書くと、あきらかに式-81は
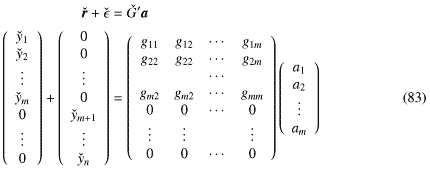 のときにϵが最短になる(ϵがすべての列ベクトルと直交している)。
のときにϵが最短になる(ϵがすべての列ベクトルと直交している)。
これはすなわち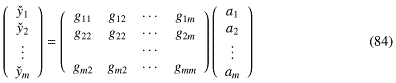 の解aを求めればそれがチェック付きyにもっとも近いチェック付きrとなって、その残差がチェック付きϵである、ということになる。つまり式-84は、実質的には式-32(大昔のここにある)と同じものであり、その解aは式-79の最小2乗解である、ということになる。
の解aを求めればそれがチェック付きyにもっとも近いチェック付きrとなって、その残差がチェック付きϵである、ということになる。つまり式-84は、実質的には式-32(大昔のここにある)と同じものであり、その解aは式-79の最小2乗解である、ということになる。
前回まではGivens回転やHouseholder変換は対称行列に対して行ったけど、非対称行列にも可能なので、式-81のQをGivens回転やHouseholder変換を使って、さっきと全く同じことをしてやると式-83は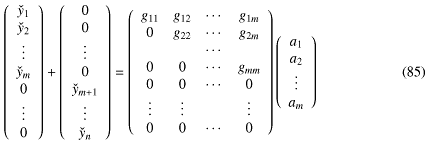 とすることができて、従って式-84は
とすることができて、従って式-84は
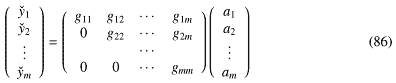 となって、このまま後退代入の可能な形になる。
となって、このまま後退代入の可能な形になる。
最初のやり方ではtG Gを作るところでかけ算回数はn ×m2で、householder行列のuを作るために列ごとに2m回、上三角行列を作るのに列ごととyに対して2m回かけ算がある。従って後退代入の前まででおおよそnm2+4m(m+1)回のかけ算が必要である。 不能の方程式から直接出発するとtG Gの計算はなくなるが、householder行列の大きさがm ×mからn ×nになるので、uを作るために列ごとに2n回、上三角行列を作るのに列ごととyに対して2n回かけ算がある。従って後退代入の前まででおおよそ2n(2m+1)回のかけ算となる。
不能の方程式から出発したほうがかけ算回数が減る条件は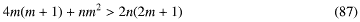 となる。左辺のほうはmについて2次だが、右辺は1次であきらかにmの大きなところで不等式が成り立つと直感的にわかる。nはすごく大きな数だとして、ざっくり数値評価すればm > 5では不能の方程式から直接計算するほうがかけ算の回数は少ない、ということになる。ようするに決定したい変数の数が多くなれば正規方程式より、不能の方程式からのほうが計算効率上は有利、ということになる。
となる。左辺のほうはmについて2次だが、右辺は1次であきらかにmの大きなところで不等式が成り立つと直感的にわかる。nはすごく大きな数だとして、ざっくり数値評価すればm > 5では不能の方程式から直接計算するほうがかけ算の回数は少ない、ということになる。ようするに決定したい変数の数が多くなれば正規方程式より、不能の方程式からのほうが計算効率上は有利、ということになる。
また、不能の方程式から出発すればtG Gの計算がなくなって手順としては一手間減ることになる。最小2乗法のように確立された実装がいっぱいあって結果の確認が簡単なアルゴリズムの場合はそれほど大きなメリットにはならないけど、一般の数値計算ソフトの開発では正しい結果がわからないことも多いので、数値計算で「一手間減る」というのは重要な場合が少なくない。こういうところでその嗅覚を養っておく、というのも若い人にはいいことではないかと思ったりもする。
しかし、なんで同じ問題で同じ行列にたどり着くのに、こんな差がでるのかよくわからない。
このへん詳しい人、教えて。
3.7 QR分解から解を得る
具体的な計算に対するちょっとした補足をする。以前の説明では
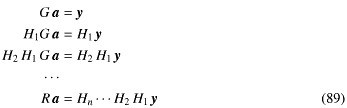
4 不能の1次方程式から
これまでは最小2乗法の正規方程式を解くことを考えてきた。これは式の数と未知数の数の一致しているので、もしすべての列ベクトルが独立なら(行列がフルランクなら)原理的には解がある。ここではちょっと見方を変えて、式-26(昔のここにある)の不能の方程式から出発してみる。もう一度書いてみると、n > mのときに
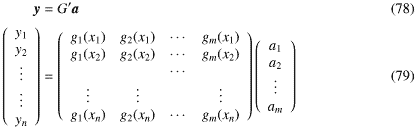
この部分空間Rmを、n次元の直交行列QをかけてRnのなかのn−m個の軸の成分を0にすることを考える。つまり3次元空間内の2次元空間の場合では図-16のような変換をするということである。

これができれば、式-79は

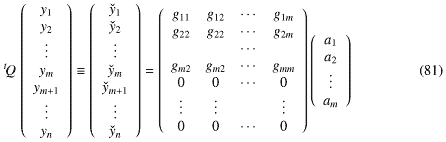

これはすなわち

前回まではGivens回転やHouseholder変換は対称行列に対して行ったけど、非対称行列にも可能なので、式-81のQをGivens回転やHouseholder変換を使って、さっきと全く同じことをしてやると式-83は


4.1 演算回数の比較
演算回数をざっくり比較してみる。後退代入をする前まではほとんどがベクトルの内積計算なので、かけ算と足し算の回数はほぼ同じである。最初のやり方ではtG Gを作るところでかけ算回数はn ×m2で、householder行列のuを作るために列ごとに2m回、上三角行列を作るのに列ごととyに対して2m回かけ算がある。従って後退代入の前まででおおよそnm2+4m(m+1)回のかけ算が必要である。 不能の方程式から直接出発するとtG Gの計算はなくなるが、householder行列の大きさがm ×mからn ×nになるので、uを作るために列ごとに2n回、上三角行列を作るのに列ごととyに対して2n回かけ算がある。従って後退代入の前まででおおよそ2n(2m+1)回のかけ算となる。
不能の方程式から出発したほうがかけ算回数が減る条件は
また、不能の方程式から出発すればtG Gの計算がなくなって手順としては一手間減ることになる。最小2乗法のように確立された実装がいっぱいあって結果の確認が簡単なアルゴリズムの場合はそれほど大きなメリットにはならないけど、一般の数値計算ソフトの開発では正しい結果がわからないことも多いので、数値計算で「一手間減る」というのは重要な場合が少なくない。こういうところでその嗅覚を養っておく、というのも若い人にはいいことではないかと思ったりもする。
しかし、なんで同じ問題で同じ行列にたどり着くのに、こんな差がでるのかよくわからない。
このへん詳しい人、教えて。
2014-06-20 22:16
nice!(0)
コメント(0)
トラックバック(0)


コメント 0