最小2乗法 - その12 [最小2乗法のイメージ]
いちおう数学は終わって、設計もおおまかにはできたので、実装する。今回はやはりAppleのdeveloper programに参加してはじめてのコードだし、これからも書き続けようと思うので、Cocoa/Objective-Cの新しい(ちっとも新しくない、と言われるだろうけど)機能をちゃんと使うことにしよう。
それはつまり
一番の山はARCで、慣れの問題が大きい。ちゃんとAppleのガイドラインに従ったコーディングをしてるつもりなんだけど、特にinitの中でmalloc()したメモリをdeallocでfree()するところでクラッシュしたりする。まだよくわかっていないらしい。MRC(Manual RC)ではこういうバグはまず出さないくらい慣れてきたのに。まあ、しょうがない。
今回はじめて知ったんだけど、ARCは32ビットモードでは動かないらしい。ARCはコンパイラの機能なので32/64ビットには関係ないし、MRCとコンパイル単位レベルで互換性があるはずなんだけど、Objective-Cのランタイムが対応していないとコンパイラが言う。
改めて見直してみるとシステムのFrameworkでも昔からあるのは32/64ビットのユニバーサルバイナリだけど、例えばAVKitやMapKit、GameController、SpriteKit、EventKitなんかがすでに64ビット単一のバイナリになっている。OS Xのシェアの問題からサードパーティがマルチプラットフォームを前提にするせいで、AppleはOSの新しい機能を使ってもらいにくい状況にある。Adobeなんかの大手のソフトは32ビットモードがまだまだ残っている。なるほどなあ。強力な64ビット化圧力だなあ。でも同じことをMicrosoftがWindowsでやると非難ごうごうだろうなあ。
Householder変換によるQR分解を使った最小2乗法はいろんなところでやってるので、いまさら実装そのものが面白いわけではない。ということで実装の詳細はソースをみてもらうということにする。
今回やってみたいのは、ガウスの消去法に比べてQR分解による最小2乗法がどのくらい数値的に安定か、を比較すること。案外そういうことをしているのをみたことがない。
前にも書いたように連立方程式を解く、という面からみると最小2乗法は数値的に不安定になりやすい問題だった。すなおなガウスの消去法ではどのくらい不安定、つまり結果の精度がどのくらい劣化して、QR分解だとそれがどのくらいマシになるかをみてみたい。
ということで、よくあるベキ展開を考える。
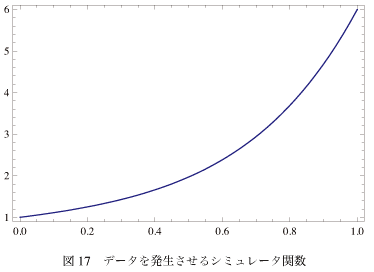
もとのデータは実際には例えば測定結果の数字なんかになるわけだけど、今回はそのシミュレーションとして1次元の関数f(x)から作る。そのシミュレータ関数は簡単のため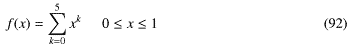 としよう。つまり係数全部が1の5次までのベキ和である。これは図-17みたいな形になる。これといった特徴のない単調増加の関数で、これからほんとに6つの係数が決められるのか不思議な気もする。
としよう。つまり係数全部が1の5次までのベキ和である。これは図-17みたいな形になる。これといった特徴のない単調増加の関数で、これからほんとに6つの係数が決められるのか不思議な気もする。
 最小2乗法でベキフィットしたときに、結果が見やすい(1と比べればいい)のでとりあえずこうしよう。
最小2乗法でベキフィットしたときに、結果が見やすい(1と比べればいい)のでとりあえずこうしよう。
これにてきとうな数値列xnとそこでのこの関数の値の組 と、モデル関数
と、モデル関数
 から、正規方程式
から、正規方程式
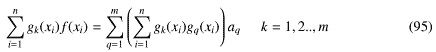 を作って、
を作って、
 として、標準偏差がσで平均値が0の誤差をランダムに発生させてデータをふらつかせる。この誤差が正規分布しているなら最小2乗法は正しい値を導くはずである(データ点が十分多いとして)。
として、標準偏差がσで平均値が0の誤差をランダムに発生させてデータをふらつかせる。この誤差が正規分布しているなら最小2乗法は正しい値を導くはずである(データ点が十分多いとして)。
また、どちらもピボッティングなどの操作はしていない。
誤差なしで近似するモデル関数の方も5次まで(6項)とすると結果は
となって、(この表示桁の程度では)きれいに1が並んだ。これ以上近似するモデル関数の次数をあげると、のこりは0が並ぶはずである。6次までの場合は
となって、ちゃんと0になる。
もっと次数を上げてみると
となって、だんだん怪しくなってくる。
もう少しわかりやすくするために、得られた係数akから評価関数G(ak)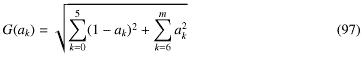 という値を使って比較しよう。つまりG(ak)の値が大きいほどもとの関数からずれている、ということになる。
という値を使って比較しよう。つまりG(ak)の値が大きいほどもとの関数からずれている、ということになる。
図-18に次数に対するG(ak)の値をプロットしたものを示す。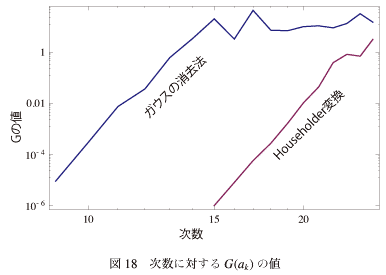 なぜ単調にあがっていかないのかよくわからないけど、傾向としてはどちらも次数を増やすと増加傾向にある。次数が低いうちはガウスの消去法は桁違いに悪い、ということがわかる。
なぜ単調にあがっていかないのかよくわからないけど、傾向としてはどちらも次数を増やすと増加傾向にある。次数が低いうちはガウスの消去法は桁違いに悪い、ということがわかる。
次数があがってくるとHouseholder変換も悪くなってくるが、これはあとで考察する。
次回は、これに誤差をまぜたときにどうなるか、そのあと今回僕が一番言いたかったことを書いて最小2乗法に関してはおしまいにする。
それはつまり
- ARC(Automatic Reference Counting)
- property
- block
- 無名カテゴリ(ほんとは「クラス拡張」というらしいけど、このほうが僕にはわかりやすい)
一番の山はARCで、慣れの問題が大きい。ちゃんとAppleのガイドラインに従ったコーディングをしてるつもりなんだけど、特にinitの中でmalloc()したメモリをdeallocでfree()するところでクラッシュしたりする。まだよくわかっていないらしい。MRC(Manual RC)ではこういうバグはまず出さないくらい慣れてきたのに。まあ、しょうがない。
今回はじめて知ったんだけど、ARCは32ビットモードでは動かないらしい。ARCはコンパイラの機能なので32/64ビットには関係ないし、MRCとコンパイル単位レベルで互換性があるはずなんだけど、Objective-Cのランタイムが対応していないとコンパイラが言う。
改めて見直してみるとシステムのFrameworkでも昔からあるのは32/64ビットのユニバーサルバイナリだけど、例えばAVKitやMapKit、GameController、SpriteKit、EventKitなんかがすでに64ビット単一のバイナリになっている。OS Xのシェアの問題からサードパーティがマルチプラットフォームを前提にするせいで、AppleはOSの新しい機能を使ってもらいにくい状況にある。Adobeなんかの大手のソフトは32ビットモードがまだまだ残っている。なるほどなあ。強力な64ビット化圧力だなあ。でも同じことをMicrosoftがWindowsでやると非難ごうごうだろうなあ。
5.3 実装結果
ということで、さくっと実装して動作を確かめよう。Householder変換によるQR分解を使った最小2乗法はいろんなところでやってるので、いまさら実装そのものが面白いわけではない。ということで実装の詳細はソースをみてもらうということにする。
今回やってみたいのは、ガウスの消去法に比べてQR分解による最小2乗法がどのくらい数値的に安定か、を比較すること。案外そういうことをしているのをみたことがない。
前にも書いたように連立方程式を解く、という面からみると最小2乗法は数値的に不安定になりやすい問題だった。すなおなガウスの消去法ではどのくらい不安定、つまり結果の精度がどのくらい劣化して、QR分解だとそれがどのくらいマシになるかをみてみたい。
ということで、よくあるベキ展開を考える。
もとのデータは実際には例えば測定結果の数字なんかになるわけだけど、今回はそのシミュレーションとして1次元の関数f(x)から作る。そのシミュレータ関数は簡単のため

これにてきとうな数値列xnとそこでのこの関数の値の組
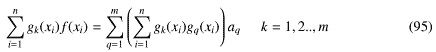
- ガウスの消去法
- Householder変換を使ったQR分解
結果の比較
比較のための計算の精度はdouble(倍精度)を使った。float(単精度)でやればもっと差がはっきりしたかもしれない。データ点数は1000点(0.001きざみ)で行った。また、どちらもピボッティングなどの操作はしていない。
5.4.1 次数による違い
データは5次までのベキだけど、近似するモデル関数の方はもっと次数が高くてもいい。次数が高くなると条件数はどんどん悪くなるので、ガウスの消去法では不利になるはずである。誤差なしで近似するモデル関数の方も5次まで(6項)とすると結果は
| 0次 | 1次 | 2次 | 3次 | 4次 | 5次 | |
| ガウスの消去法 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| Householder変換 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| 0次 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次 | |
| ガウスの消去法 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | -0.00000 |
| Householder変換 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 0.00000 |
もっと次数を上げてみると
| 0次 | ... | 6次 | 7 | 8 | 9 | 10 | |
| ガウスの消去法 | 1.00000 | ... | 1.00011 | -0.00018 | 0.00018 | -0.00009 | 0.00002 |
| Householder変換 | 1.00000 | ... | 1.00000 | -0.00000 | 0.00000 | -0.00000 | 0.00000 |
もう少しわかりやすくするために、得られた係数akから評価関数G(ak)
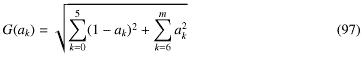
図-18に次数に対するG(ak)の値をプロットしたものを示す。

次数があがってくるとHouseholder変換も悪くなってくるが、これはあとで考察する。
次回は、これに誤差をまぜたときにどうなるか、そのあと今回僕が一番言いたかったことを書いて最小2乗法に関してはおしまいにする。
2014-06-28 20:44
nice!(0)
コメント(0)
トラックバック(0)


コメント 0