ガウシアンビームの光学 - その18

ガウシアンビームのお話。これまで「その1」から「その15」まででガウシアンビームの教科書的なあつかいを（ダラダラと）まとめた。そのあと光学に固有の問題のためにまず代表的な数値の確認と基礎となる近軸理論を簡単にすませた。今日はもう少し具体的に、光学系の瞳から出たガウシアンビームがその先でウェストを迎えるところをイメージしてみる．．．．

6.2.2  瞳上でビーム半径を与えた場合

汎用的なやりかたはあとでまとめるとして、とりあえずこの図

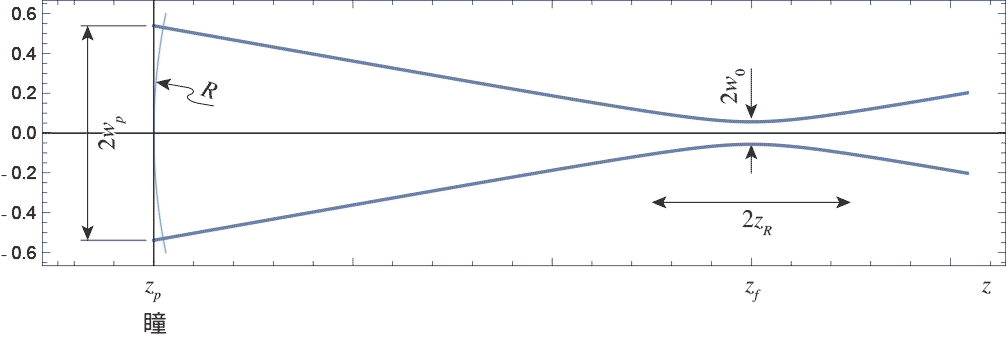のように光学系の射出瞳での$1/e^2$半径が決まっていて、そのあとのどこにどんなウェストを作ることができるか、を考えてみる。

射出瞳の中心を原点にとって、瞳からガウシアンビームが射出されるとする。瞳でのビームの$1/e^2$半径を$w_p$とする。そしてもちろん射出瞳の半径は$w_p$に比べて十分大きい（絞りでケラれない）とする。そして$z=z_f$の位置に半径$w_0$のウェストができたとする。まずこのときの$w_p$と$w_0$の関係を調べてみる。

ずっと前ガウシアンビームを導いて式を整理したときにでてきた \begin{equation} w(z) = w_0 \sqrt{ 1+(z/z_R)^2} \nonumber \end{equation} が、ある$z$の位置$z=z_p$でのビーム半径になっていて、それが瞳位置だと考えればいい。そうすると \begin{equation} w_p = w(z_p) \end{equation} として$w_0$について解けばいい。実際にやってみると \begin{align} w_p &= w_0 \sqrt{1+\left(\frac{z_p}{z_R} \right)^2} \nonumber \\ &= w_0 \sqrt{1+\left( \frac{\lambda z_p}{\pi w_0^2} \right)^2} \nonumber \\ w_0 &= \sqrt{\frac{w_p^2 \pm \sqrt{\displaystyle w_p^4 - \left(\frac{2\lambda z_p}{\pi} \right)^2 }}{2}} \label{waistsolution} \end{align} となって解は2個でてくる（ほんとは4つあるけど、符号の違いだけなので正のほうだけ考えればいい）。

まずこの解の形では、2重根号になっていて（2重根号が煩わしいけど解けない）内側の根号の中身は負になり得て、そのときは解ではない。それを除いておく必要がある。この中身が負にならないためには \begin{equation} \pi w_p^2 \geq 2\lambda |z_p| \nonumber \end{equation} でなければならない（$w_p$や$\lambda$は定義から負にはならないので2次式を解いた）。$z_p$はウェストから瞳までの距離だったので、これはすなわち瞳での半径を決めてしまうと、ウェストの位置はあるところ以上遠くにはできない、ということになる。その位置$z_p \le z_L$は \begin{equation} z_L = \pm \frac{\pi w_p^2}{2\lambda} \label{farthest} \end{equation} となって、なんとなく見覚えのある式になる。

$z=z_L$で式-\ref{waistsolution}の2個の解は \begin{equation} w_0 = \frac{w_p}{\sqrt{2}} \nonumber \end{equation} となって瞳でのビーム半径でウェスト半径は決まってしまう。これで式-\ref{farthest}を書き換えると \begin{equation} z_L = \pm \frac{\pi w_0^2}{\lambda} \equiv \pm z_R \end{equation} となって、瞳での半径が決まっていてなるべく瞳からウェストを遠ざけようとすると、瞳がRayleigh領域の端になる場合が最も遠くなる、という結果である。もしそれ以上遠くに作りたいなら、瞳でのビーム半径を大きくする必要がある、ということで定性的には回折を考えると当然、という感じの結果ではあるけど、それがちょうど$z_R$というのは面白い。つまりその意味においても$z_R$が特徴的な量だ、ということである。

もう少し詳しく見てみる。式-\ref{waistsolution}のふたつの解はどう違うのだろう。ひとつめの根号の中の符号に従って \begin{align} w_{-0}(z_p) &= \sqrt{\frac{w_p^2 - \sqrt{\displaystyle w_p^4 - \left(\frac{2\lambda z_p}{\pi} \right)^2 }}{2}} \\ w_{+0}(z_p) &= \sqrt{\frac{w_p^2 + \sqrt{\displaystyle w_p^4 - \left(\frac{2\lambda z_p}{\pi} \right)^2 }}{2}} \label{waistsolution2} \end{align} としておこう。

これが$z$に関してどんな形をしているのかプロットしたのがこの図である。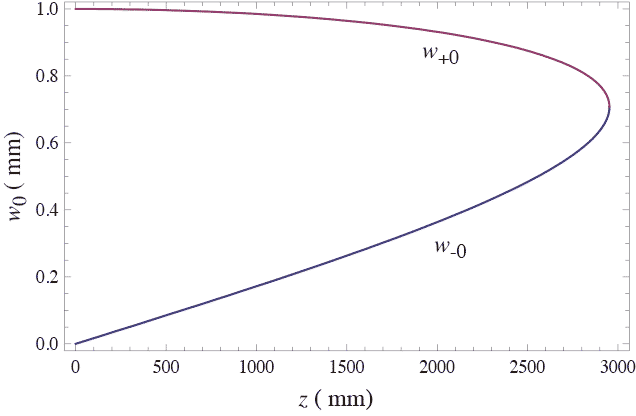

図では波長が532nm、瞳でのビーム半径が1mmの場合である。式からもわかるように$w_{-0}$のほうは瞳付近で0に近づいていく。これは一見おかしいように思えるけど、$z$を小さくしていく、ということはウエストの位置をどんどん瞳に近づけていく、つまりどんどんN.A.を高くしていきながら絞り込んでいく、ということになっている。従って$z=0$では無意味であるが、その近くでは非常に高いN.A.で小さなスポットを作ることに対応していて、以前計算した$z_R$の下限の条件を満足するなら解としては正しい、ということになる。

一方の$w_{+0}$のほうは$z=0$で$w_{+0}=w_p$であって、これはただ瞳から平行光ででていく場合に対応することがわかるので、ようするに瞳がRayleigh領域の中にある場合である。

つまり$w_{-0}$の$z \approx 0$の付近を除いて両方とも物理的に意味のある解であって、$w_{-0}$は瞳がRayleigh領域の外となる場合で、$w_{+0}$は内側になる場合ということになる。