ガウシアンビームの光学 - その26 [ガウシアンビーム]
ガウシアンビームの続き。「その1」から「その15」までに教科書的な話をして、代表的な数値の確認、近軸理論、瞳から出たガウシアンビームがウェストを迎える様子、$z$、$z_R$とは別のパラメータ、ガウシアンビームの場の特定法、近軸マトリクスのおさらい、近軸理論との齟齬、近軸マトリクスによるガウシアンビームの伝播計算とその個人的な印象、収差がある場合のウェスト付近の場とやってきた。今日はFraunhofer回折を計算するときのコツについて。これはどっちかというとガウシアンビームに限らない一般的な話....
被積分関数は波動方程式に従う場なのでもともと非常に滑らかで、それを絞りで切っているので、その外の場の量は0であって積分範囲を有限にすることで問題が発生することはない。ただし離散化と組み合わさるとエイリアシングという厄介な現象がおきてしまう。
具体的なFourier変換の数値計算ではいくつかのコツ、というかtipsがある。
素直に考えれば次の図の左のように配列の中心に配置するだろう。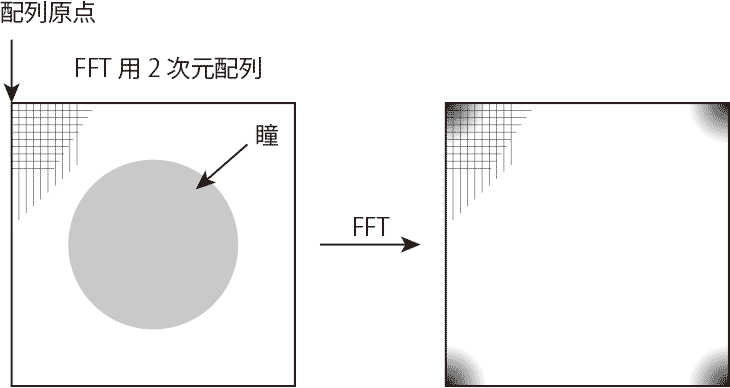 しかしそれを普通のアルゴリズムのFFTを実行すると右のようになる。なぜこうなるのかは離散化と積分範囲の有限化のせいで折り返しが発生するためで、詳細は離散Fourier変換の教科書を確認してもらいたい。
しかしそれを普通のアルゴリズムのFFTを実行すると右のようになる。なぜこうなるのかは離散化と積分範囲の有限化のせいで折り返しが発生するためで、詳細は離散Fourier変換の教科書を確認してもらいたい。
さらにこの隣り合う離散化点の位相差が$\pi$前後になる。強度だけを問題にするなら位相は気にする必要はないが、気持ち悪い。
そこで普通はこの図のようにする。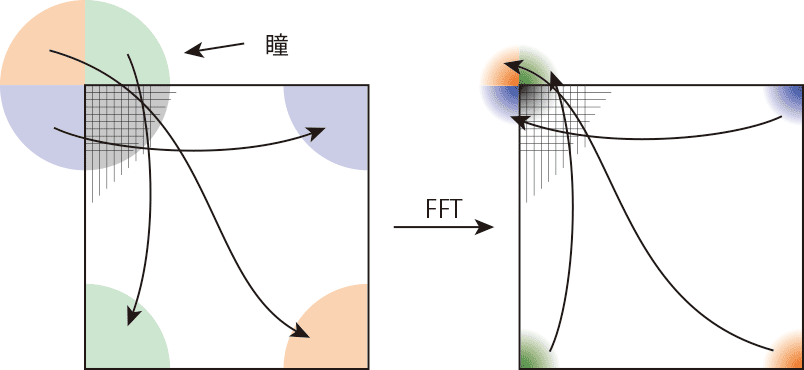 FFTのいわゆるDC成分が配列の先頭になるため(FFT後のDC成分はFuraunhofer回折との関係を考えると傾きのない点、すなわち光軸上の点に対応する)、そこが瞳面上でも光軸になるように配置すると位相の大きな回りはないし(位相の回りは瞳上での横ずらしに対応する)、瞳と焦点面とで対称なあつかいにできる。
FFTのいわゆるDC成分が配列の先頭になるため(FFT後のDC成分はFuraunhofer回折との関係を考えると傾きのない点、すなわち光軸上の点に対応する)、そこが瞳面上でも光軸になるように配置すると位相の大きな回りはないし(位相の回りは瞳上での横ずらしに対応する)、瞳と焦点面とで対称なあつかいにできる。
なぜこれでいいか、はまた離散Fourier変換の教科書を確認してもらいたい。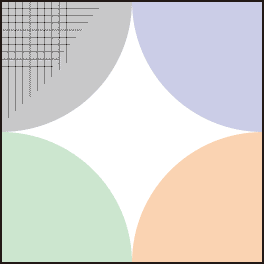 sinc補間は、FFTの結果の配列の値を$\mathcal{E}_{n,m}$、焦点面での実距離での位置$(\xi,\eta)$の場の大きさを$\mathcal{E}(\xi,\eta)$とすると
\begin{equation}
\mathcal{E}(\xi,\eta) = \sum_{n,m} \mathcal{E}_{n,m}{\rm sinc}\left(\pi (\frac{\xi}{p}-n) \right){\rm sinc}\left(\pi (\frac{\eta}{p}-m) \right)
\label{sincinterpolation}
\end{equation}
とすればいいけど、これは配列全部を対象に考えると計算量が多く、逆に瞳面で外部の0を足してFFTを実行する方がずっと速い(sinc補間をFFTで実装する場合があるくらいである)。
sinc補間は、FFTの結果の配列の値を$\mathcal{E}_{n,m}$、焦点面での実距離での位置$(\xi,\eta)$の場の大きさを$\mathcal{E}(\xi,\eta)$とすると
\begin{equation}
\mathcal{E}(\xi,\eta) = \sum_{n,m} \mathcal{E}_{n,m}{\rm sinc}\left(\pi (\frac{\xi}{p}-n) \right){\rm sinc}\left(\pi (\frac{\eta}{p}-m) \right)
\label{sincinterpolation}
\end{equation}
とすればいいけど、これは配列全部を対象に考えると計算量が多く、逆に瞳面で外部の0を足してFFTを実行する方がずっと速い(sinc補間をFFTで実装する場合があるくらいである)。
収差があまり大きくない、あるいは瞳内の強度分布が大きく変化しない、などで焦点面で場があまり広がらず、光軸付近だけを対象に(式-\ref{sincinterpolation}の$n$、$m$、$N-n$、$N-m$の小さな値だけについて)足し算してあとは無視しても十分な精度が得られるなら、$Q=2r_p$でもいいだろう。十分かどうか、必要な$n$、$m$の値の範囲はどのくらいか、なんて考えるとめんどくさいので、似たような計算をループで繰り返すなど(例えばでフォーカスを刻んで焦点前後の分布を細かく計算するなど)でなければ、何も考えずにFFT領域を広げた方が簡単だとは言える。
というわけで、これで収差がある場合の焦点面とその前後での場の様子を数値計算で求めることができるようになった。原理的には。
次にケラれの効果を考えてみる。
7.4 Fraunhofer回折のための数値計算のコツ
焦点位置付近の様子を数値計算でみようと思ったとき、もともとのFraunhofer回折の計算は式-25:2のように連続な場の無限大の範囲の積分なのでそのままでは数値計算するわけにはいかない。従って有限の範囲の積分に限定した上で離散化して数値計算を実行することになる。被積分関数は波動方程式に従う場なのでもともと非常に滑らかで、それを絞りで切っているので、その外の場の量は0であって積分範囲を有限にすることで問題が発生することはない。ただし離散化と組み合わさるとエイリアシングという厄介な現象がおきてしまう。
具体的なFourier変換の数値計算ではいくつかのコツ、というかtipsがある。
7.4.1 数値計算にはFFTを使う
というのはコツというか当然である。定義通りの計算に比べたらもちろんだし、最適化のされかたによってもかなり違う。昔みたように点数が多くなるほど効率は圧倒的である。7.4.2 瞳の配置
Fraunhofer回折の計算では射出瞳(絞りの像)が丸いのでたいてい2次元をあつかう。2次元FFTでは矩形(たいていは正方形)の領域になるのでそこへ射出瞳をどう配置するかがちょっとした問題になる。素直に考えれば次の図の左のように配列の中心に配置するだろう。

さらにこの隣り合う離散化点の位相差が$\pi$前後になる。強度だけを問題にするなら位相は気にする必要はないが、気持ち悪い。
そこで普通はこの図のようにする。

なぜこれでいいか、はまた離散Fourier変換の教科書を確認してもらいたい。
7.4.3 配列と瞳の大きさの関係
FFT配列(簡単のため正方行列とする)の一辺の点数を$N$とし、その瞳面上での長さを$Q$とする。FFTによって配列の点数は変わらない。光の波長を$\lambda$、瞳から焦点面に収束するようなビームだとして、瞳から焦点面までの距離を$z_0$として、焦点面でのサンプリング距離(配列の隣り合う点の実距離)を$p$とすると \begin{equation} p=\frac{z_0 \lambda}{Q} \end{equation} となる。したがって焦点面での配列の領域の一辺の長さを$L$とすると \begin{equation} L=N p \equiv \frac{N z_0 \lambda}{Q} \end{equation} である。$N$は$2^n$にするのが効率がいいけど、そうすると$Q$か$L$かのどちらかが中途半端な値になる。とすると計算したあとの扱いを考えると$p$がキリのいい値になっているのが便利である。瞳の実半径を$r_p$として、均一な強度分布の無収差2次元円形開口のFraunhofer回折によるスポットサイズ$S$(Airy直径)は \begin{equation} S \approx 1.22 \frac{z_0 \lambda}{r_p} \end{equation} となる。$Q$を大きくすると分解能$p$が小さくなり、$N$を大きくすると$L$が大きくなるので、これが \begin{equation} p \ll S \ll L \end{equation} となるように$N$や$Q$を調整してやればいい、ということになる。7.4.4 瞳の外側の広さ
そうやって$Q$と$N$とを選んだとする。しかし瞳の外の値は0なので、$Q$を大きくしても実質的な情報が増えたことにはならない。そう考えると下の図のように瞳を配列いっぱいいっぱいにして、FFTを実行して、その結果をsincで補間すればいい、ということになる。
収差があまり大きくない、あるいは瞳内の強度分布が大きく変化しない、などで焦点面で場があまり広がらず、光軸付近だけを対象に(式-\ref{sincinterpolation}の$n$、$m$、$N-n$、$N-m$の小さな値だけについて)足し算してあとは無視しても十分な精度が得られるなら、$Q=2r_p$でもいいだろう。十分かどうか、必要な$n$、$m$の値の範囲はどのくらいか、なんて考えるとめんどくさいので、似たような計算をループで繰り返すなど(例えばでフォーカスを刻んで焦点前後の分布を細かく計算するなど)でなければ、何も考えずにFFT領域を広げた方が簡単だとは言える。
というわけで、これで収差がある場合の焦点面とその前後での場の様子を数値計算で求めることができるようになった。原理的には。
次にケラれの効果を考えてみる。
2017-10-01 21:25
nice!(0)
コメント(0)


コメント 0