ガウシアンビームの光学 - その29 [ガウシアンビーム]
先に片付けたいことができたので、ちょっと間が空いてしまったけど、片付け終わったのでガウシアンビームの続き。
前回までで基礎的な数学と物理的な意味、光学でのあつかいなんかをやってきて、だいたい僕が仕事でやっているレーザにまつわる計算の一般論みたいなものができたというつもりでいる。会社に若い後輩がいて、こういうことを基礎知識、というより教科書だけではないボディランゲージも含めたスタイルとして伝えられればいいんだけど、今いる会社に若い奴はいない、というか光学屋は僕一人なので、こういうところに書き散らすだけになってしまう。ちょっと寂しいというか、虚しい。
前の会社なら若いのもいたんだけど。まあ最近の若いのはそういうのを落語の内弟子みたいなもののように感じて敬遠するかもしれない。僕自身も他人との濃厚接触は、還暦を過ぎた今となってもすごく苦手だし。
まあそれはいいとして、今日からシメの測定の話をする。鍋で言うなら雑炊のような話だけど（そう言う比喩でいうと数学は昆布の出汁で物理の味わいは河豚の身で光学は白菜椎茸ネギ豆腐である）、本物の雑炊と違ってそのままだとかなりドロドロするので、うまくまとまった話になるかどうかよくわからないけど、始める．．．．．
なんのためにガウシアンビームを測定する必要があるのか、というと現物のガウシアンビームからそのパラメータ、$z_R$や$z$、あるいは$\chi(z)$や$R(z)$の値を知りたい、ということがある。
もうひとつは現実の収差やケラれといった摂動によってどのくらい理想的なガウシアンビームからずれているか、というのを知りたいということである。
とくに後者の摂動の影響は、レーザを製品として売り買いする場合に必要となる。つまりレーザを使う側は、それが理想的なガウシアンビームだとみなせるならこれまでやってきた計算がそのまま使えて、簡単になる。理想的とみなせるかどうか、あるいはどのくらい理想からはずれているか、ということが使う側として重要となる。そこで提供する側に測定しろ、と要求することになる。
摂動のふたつめはどの高次モードがどういう位相と強度比（振幅比）で重なるかにもよるけど、前にちょっとだけ紹介したエルミートやラゲールの単一の高次モードは$1/e^2$幅でビーム太さを表すと、0次のモードよりも必ず太い。このことはエルミートに関してあとでちょっとだけ計算してみる。
そして、高次モードの重畳もここでは「摂動」とみなせるくらい0次が支配的である、とする。そうすると位相の関係によらず$1/e^2$幅は必ず太るだろう（高次になるほどエネルギー分布は光軸から離れる）。そのはずなんだけど、これどうやったら言えるのかな。
残りのふたつは前回まででさらっとやった。従って上の摂動のどの場合も、基本的にはウェストは太る方向である。しかし簡単に太るふとる、と言ってもビームのパラメータの違い、つまり$z_R$や$z$の違いまで含めるとなんらかの基準を設定しないと厳密な比較は難しい。
比較のための基準も含めてこれからゆっくり順番に考えていく。
ガウシアンビームの状態を表すパラメータとして$z_R$と$z$のふたつがあった。光軸を$z$軸にとったときにこのふたつ（あるいはそれに従属なパラメータ）を決めると場は一意に確定した。
ただしそれは波長をひとつに決めたときの話である。$\lambda$と$k$は波動方程式を変数分離したときの分離定数なので、そのあとの議論は暗黙のうちに「ある$\lambda$と$k$に関して」という制限がずっとついてきていたが、ここで違う波長を考えてみる。 別の波長$\breve{\lambda}$を \begin{equation} \breve{\lambda} \equiv M^2 \lambda \label{differentlambda} \end{equation} として式を書いてみる。$M (> 0)$は倍率を表す定数で2乗しているのはあとの式が見やすくなるためにそうしているだけである。ある$z_R$に対して全てを書き換えるとどうなるか考えてみる。
波長はそのあとの議論でずっと定数だとみなしていて、波長の違いは全ての式で式-\ref{differentlambda}の置き換えをするだけになる。例えばビームウェスト半径$\breve{w}_0$は \begin{equation} \breve{w}_0 = M\sqrt{\frac{\lambda z_R}{\pi}} \equiv M w_0 \end{equation} だし、それ以外のビーム半径$\breve{w}(z)$は \begin{equation} \breve{w}(z) = M w_0 \sqrt{1+\left(\frac{z}{z_R}\right)^2} \equiv M w(z) \end{equation} で、広がり角$\breve{\theta}$は \begin{equation} \breve{\theta} = M \frac{w_0}{z_R} \equiv M \theta \end{equation} となる。
つまりRayleigh長さ$z_R$が同じなら波長が$M^2$倍のガウシアンビームのこれらの値は$M$倍になる、ということである。次の図にある波長とその2倍の波長の場合のウエスト付近のビーム幅の変化を示した。同時に点線で$x$方向の強度分布を示してある。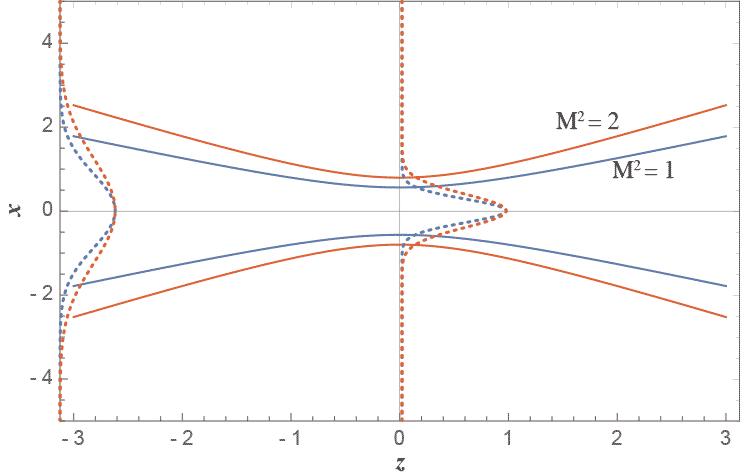
一方、例えば波面の曲率半径$R(z)$やGouy位相$\zeta(z)$はナマに波長が入っていないので変わらない、つまり同じ$z_R$なら波長が違ってもこれらは同じだということになる。
Gouy位相はともかく、ビームはウェストに向かって収束してきて、そのあと発散していくんだから$R(z)$が変わらないというのは当然だろう。
ところで、$M^2$が2なんて例を考えると、波長の違いを「摂動」というのはちょっとおかしいかもしれない。本来は中心波長の周りにちょっと広がった幅がある、ぐらいですませるような議論に収めたい。それで済むかどうかは、この先に話を進めて行った結果によるので、途中で首が回らなくなるかもしれない。そのときはごめんなさい。まあ、順にやっていこう。
前回までで基礎的な数学と物理的な意味、光学でのあつかいなんかをやってきて、だいたい僕が仕事でやっているレーザにまつわる計算の一般論みたいなものができたというつもりでいる。会社に若い後輩がいて、こういうことを基礎知識、というより教科書だけではないボディランゲージも含めたスタイルとして伝えられればいいんだけど、今いる会社に若い奴はいない、というか光学屋は僕一人なので、こういうところに書き散らすだけになってしまう。ちょっと寂しいというか、虚しい。
前の会社なら若いのもいたんだけど。まあ最近の若いのはそういうのを落語の内弟子みたいなもののように感じて敬遠するかもしれない。僕自身も他人との濃厚接触は、還暦を過ぎた今となってもすごく苦手だし。
まあそれはいいとして、今日からシメの測定の話をする。鍋で言うなら雑炊のような話だけど（そう言う比喩でいうと数学は昆布の出汁で物理の味わいは河豚の身で光学は白菜椎茸ネギ豆腐である）、本物の雑炊と違ってそのままだとかなりドロドロするので、うまくまとまった話になるかどうかよくわからないけど、始める．．．．．
9 ガウシアンビームの測定
レーザから出た光を光学系に通して、絞り込んだりする場合、ちゃんとできているかを測定したい、ということがある。最後に測定の話をまとめてガウシアンビームの話を終わることにする。なんのためにガウシアンビームを測定する必要があるのか、というと現物のガウシアンビームからそのパラメータ、$z_R$や$z$、あるいは$\chi(z)$や$R(z)$の値を知りたい、ということがある。
もうひとつは現実の収差やケラれといった摂動によってどのくらい理想的なガウシアンビームからずれているか、というのを知りたいということである。
とくに後者の摂動の影響は、レーザを製品として売り買いする場合に必要となる。つまりレーザを使う側は、それが理想的なガウシアンビームだとみなせるならこれまでやってきた計算がそのまま使えて、簡単になる。理想的とみなせるかどうか、あるいはどのくらい理想からはずれているか、ということが使う側として重要となる。そこで提供する側に測定しろ、と要求することになる。
9.1 ガウシアンビームの摂動
理想的なガウシアンビームに対する摂動をもう一度整理する。- 有限の波長幅
- 高次モードの重畳
- 収差
- ケラれ
摂動のふたつめはどの高次モードがどういう位相と強度比（振幅比）で重なるかにもよるけど、前にちょっとだけ紹介したエルミートやラゲールの単一の高次モードは$1/e^2$幅でビーム太さを表すと、0次のモードよりも必ず太い。このことはエルミートに関してあとでちょっとだけ計算してみる。
そして、高次モードの重畳もここでは「摂動」とみなせるくらい0次が支配的である、とする。そうすると位相の関係によらず$1/e^2$幅は必ず太るだろう（高次になるほどエネルギー分布は光軸から離れる）。そのはずなんだけど、これどうやったら言えるのかな。
残りのふたつは前回まででさらっとやった。従って上の摂動のどの場合も、基本的にはウェストは太る方向である。しかし簡単に太るふとる、と言ってもビームのパラメータの違い、つまり$z_R$や$z$の違いまで含めるとなんらかの基準を設定しないと厳密な比較は難しい。
比較のための基準も含めてこれからゆっくり順番に考えていく。
9.2 波長の違いとM2 （M squared）
まず摂動の一つ目として波長の違いを考えてみる。ガウシアンビームの状態を表すパラメータとして$z_R$と$z$のふたつがあった。光軸を$z$軸にとったときにこのふたつ（あるいはそれに従属なパラメータ）を決めると場は一意に確定した。
ただしそれは波長をひとつに決めたときの話である。$\lambda$と$k$は波動方程式を変数分離したときの分離定数なので、そのあとの議論は暗黙のうちに「ある$\lambda$と$k$に関して」という制限がずっとついてきていたが、ここで違う波長を考えてみる。 別の波長$\breve{\lambda}$を \begin{equation} \breve{\lambda} \equiv M^2 \lambda \label{differentlambda} \end{equation} として式を書いてみる。$M (> 0)$は倍率を表す定数で2乗しているのはあとの式が見やすくなるためにそうしているだけである。ある$z_R$に対して全てを書き換えるとどうなるか考えてみる。
波長はそのあとの議論でずっと定数だとみなしていて、波長の違いは全ての式で式-\ref{differentlambda}の置き換えをするだけになる。例えばビームウェスト半径$\breve{w}_0$は \begin{equation} \breve{w}_0 = M\sqrt{\frac{\lambda z_R}{\pi}} \equiv M w_0 \end{equation} だし、それ以外のビーム半径$\breve{w}(z)$は \begin{equation} \breve{w}(z) = M w_0 \sqrt{1+\left(\frac{z}{z_R}\right)^2} \equiv M w(z) \end{equation} で、広がり角$\breve{\theta}$は \begin{equation} \breve{\theta} = M \frac{w_0}{z_R} \equiv M \theta \end{equation} となる。
つまりRayleigh長さ$z_R$が同じなら波長が$M^2$倍のガウシアンビームのこれらの値は$M$倍になる、ということである。次の図にある波長とその2倍の波長の場合のウエスト付近のビーム幅の変化を示した。同時に点線で$x$方向の強度分布を示してある。
Gouy位相はともかく、ビームはウェストに向かって収束してきて、そのあと発散していくんだから$R(z)$が変わらないというのは当然だろう。
ところで、$M^2$が2なんて例を考えると、波長の違いを「摂動」というのはちょっとおかしいかもしれない。本来は中心波長の周りにちょっと広がった幅がある、ぐらいですませるような議論に収めたい。それで済むかどうかは、この先に話を進めて行った結果によるので、途中で首が回らなくなるかもしれない。そのときはごめんなさい。まあ、順にやっていこう。
2017-12-07 21:52
nice!(0)
コメント(0)
コメント 0