SwiftのProtocolが面白い [Swiftプログラミング]
Swiftの勉強をちびちび続けている。どうせAppleのことだからSwiftのランタイムがObjective-Cのコードに依存しなくなったら、あっという間にObjective-CをObsoleteにするに違いなくて、その準備をしないといけない。この歳になって新しいことを勉強するのは厳しいけど、いまさら他のプラットフォームに移るなんてことはもっと大変なのでしょうがない。
最初、僕はSwiftを「ようするにCとおさらばしたObjective-Cという感じ」だと思っていたけど、ちゃんと勉強を始めてみると、結構Objecitve-Cとは違っていて面白い、と思うようになってきた。単に文法をすっきりさせて流行りを取り込んだだけ、というわけではないらしい。
なんとなくわかってきたのが、LLVMの解析能力をフルに使えるような工夫がいろいろあるように思えるところ。ARCはその最たるものだし、整数や実数なんか（Cではスカラ型と分類される）までStructの仲間にしておきながら、実行時のメモリや命令のオーバーヘッドはCと変わらない、というのもできる限りコンパイル時点で解析して静的に解決するような言語仕様になっているからだろう。Objective-Cとは真逆の考え方である。
さらにProtocolの位置付けがObjective-Cとはかなり違っている、というのに気がついた。特にSwift Standard Libraryに含まれる基本的なProtocolは数学のあるものによく似ている．．．．．
Protocolは最初Objective-Cのリモートなオブジェクトとの通信のオーバーヘッドを減らすために考えられた便宜的なものらしいけど、そのうちいろんなところにProtocolを見るようになっていた。例えばNSObjectのカテゴリとして緩く宣言されていたdelegateメソッドなんかもProtocolとして「使う使わない」をはっきりとさせるようになった。
Protocolは、構造体がデータをひとまとめにしたものとみなせるように、操作をひとまとめにしたものとざっくり考えていい（と僕は思っている）が、Swiftではさらに一歩踏み込んでいる。僕の理解では、Swiftでは整数までStructだとみなしたので、プログラミングで使うあらゆるオブジェクトというか実体に対して、Protocolによって可能な操作の分類を与えることができる。
なんのことを言ってるんだかわからないけど、もう少し具体的に言えば、例えば二つの整数は大小の比較ができる。また文字列も辞書順で比べれば二つの文字列に順番を与えることができる。数学の言葉で言うと整数全体の集合も文字列全体の集合も全順序集合とみなせる。全順序なら実体が整数であろうが文字列であろうが、複数の元を一意の（常に同じ）順番で並べることができて、その方法（アルゴリズム）は整数でも文字列でも同じものが使える、ということになる。この「大小の比較可能」と言う性質をSwiftでは「Comparable」というProtocolで表す。さっきの一意の順番に整列させる操作を「ソート」と言うけど、「Comparable」Protocolをconformするオブジェクトは自動的にソートが可能になる。
「Comparable」も含めて具体的なProtocolはSwiftの言語仕様には含まれていなくて、Swift Standard Libraryの一部になっているが、その言語仕様の一部はStandard libraryが前提に（たとえばfor inループとか）なっている。
「Comparable」の他にも、基本的なProtocolとして例えばふたつの元が同じかどうかが判断できる「Equatable」、その判断のためにハッシュ値を割り当てることができる「Hashable」、ふたつの元の距離が定義できる「Strideable（なんでStridableじゃないんだろう）」など、非常に基本的なものが用意されている。
こういった仕様は（JavaやRubyとかには演算子を再定義するために現れることはあるけど）これまでのプログラミング言語ではごく当たり前の、暗黙の性質だとしてあからさまには現れてこなかった。Swiftではこういう性質の分類をProtocolをconformすることに対応させている。「Comparable」ProtocolにConformするオブジェクト（なんども書くけどクラスのインスタンスだけでなくStruct以下すべで含めて）の集合に対してはひとつのソート関数だけでいいし、「Strideable」なオブジェクトだと、それが巨大なクラスのインスタンスだったとしても、例えば配列のindexに使える、ということになる。
ただし、実際の「ふたつの元の大小を判断する」ための具体的な関数はそれぞれのオブジェクトごとに実装する必要がある。Protocolはただ「ふたつの元の大小が判断できる」という性質だけを定義して、その実装は問わない、というものである。
Swift Standard Libraryの中にそういう基本的なProtocolがいくつあってそれぞれどうなっているのか、と思ってドキュメントを見てもそれぞれの記述はあるけど全体がわかるようにはなっていない。何かないかと探していると親切な人がいた。Standfard LibraryにあるStruct、Class、EnumとProtocolの継承関係をDOT言語というグラフ記述言語で網羅してくれている。gitをcloneしてくるとその中のsslcd.dotというファイルにまとめられている。こう言うのを作ってくれているのはすごくありがたい。感謝。
僕はDOT言語を知らなかったけど見ればそれほど難しくはない。でもソースだけ眺めていても全然わからないし、このためだけにgraphvizをインストールするのもイマイチなので、いつものパターンでMathematicaに読み込んでみる。
Mathematicaはグラフを表示する機能があって、DOT言語の記述も読み込める。
これを見やすいグラフに表示させる。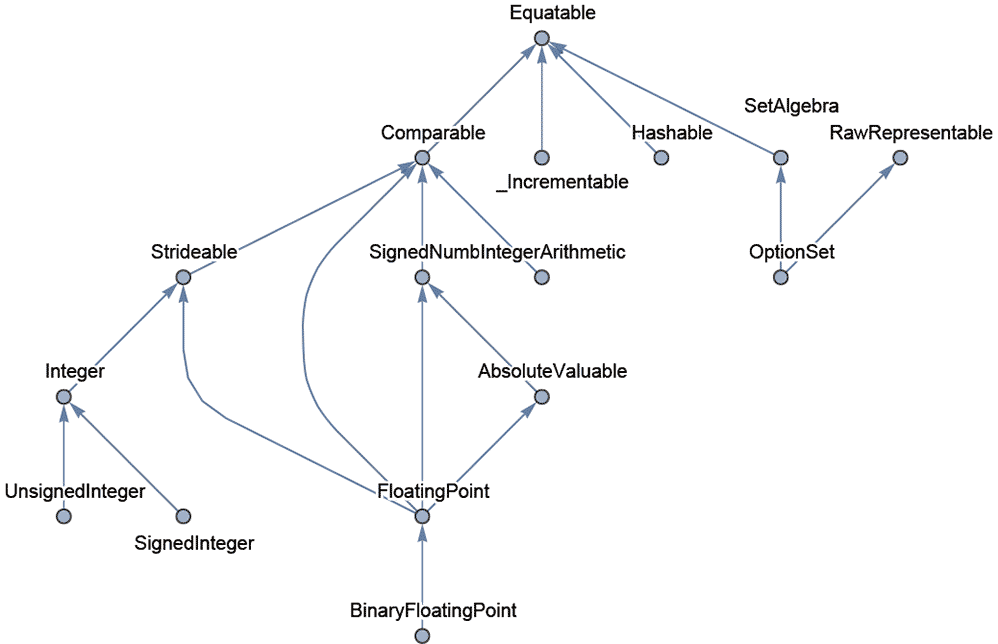
名前からそれぞれどういうものなのか、はなんとなくわかるような気がする。
ところでこのProtocolの「実装は問わずに可能な操作だけを定義する」という方針は、抽象代数に出てくる代数構造によく似ている。抽象代数では、集合の元がなんであるか、は問わずに集合が満たすべき公理を定義して、それだけから議論を展開する。例えば「群」は、集合に2項演算が定義されてその演算に関して閉じていて、その演算が結合法則を満たして、かつ単位元と逆元が存在するような集合のことである。その元は数なのか林檎なのか梨なのかそれとも別の何かなのか、その2項演算とは具体的に何をすることなのか、などということは気にしないしどうでもいい。
この群を研究する数学が群論で、たったこれだけのことから例えば5次以上の代数方程式の解の公式は作れないことが証明できたり、固体結晶の原子の並び方は（3次元では）32種類しかないことが言えたりする（ただしその証明は群の性質だけからではなくて整数の構造が反映している）。
群以外にも、群の定義のうち単位元逆元の存在しない「半群」、もっと簡単な単に2項演算が定義されているだけの「マグマ」や、逆にふたつの2項演算が定義されて、一つの演算に関してアーベル群で、もう一方がモノイドで、アーベル群の演算に対してモノイドになる演算が分配的になる、という公理を満たすものを「体」などという。体のうち元の濃度（個数）が有限のものを有限体と言って、これは誤り訂正に使われたりしている。
Wikipediaに出てくる基本的な代数構造を同じようなグラフに描いてみると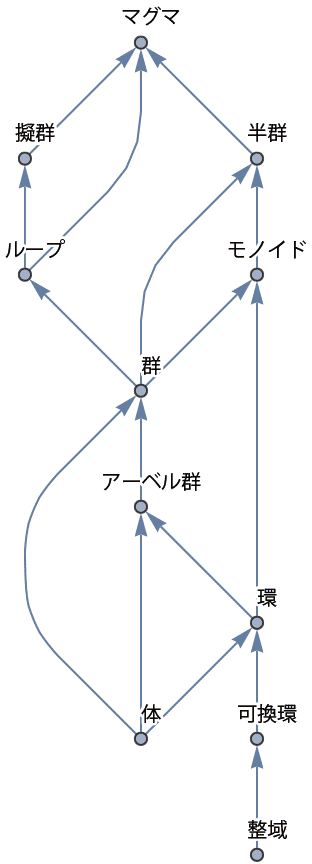
などとなる。Protocolの場合は矢印（辺、Edge）が継承関係を表していて、逆に辿ると関数が追加されることになるけど、代数構造の場合は矢印を逆に辿ると満たす公理が追加されることになる。さっきよりちょっとさみしいけど、さらにこの先には例えば位相空間、距離空間、線型空間、ノルム空間、Hilbert空間などといった解析でもおなじみの代数構造が続いて、広大な数学の枝葉が茂っている。
ちなみにこのグラフを書くMathematicaコード（上と同じにするには修正が必要）は
こうやって代数の構造と比較してみるとSwift Standard LibraryのProtocolは公理論的だ、と言える。こういうのは単に整理がつきやすいだけでなく、ある挙動がなにに基づいているか、全然別の実体が全く同じ挙動をする原因、その挙動の本質がわかったりする。例えば量子力学のシュレーディンガー方程式とハイゼンベルク方程式が見た目は全然違うのに同じ結果を返すのは何故なのか、が理解しやすくなる。
こういう公理論的な考え方はヒルベルトがやりだして、ブルバキが徹底的にやったものらしい。Siwftを設計したひとのなかにヒルベルトのファンやブルバキのシンパがいるのだろうか。他にもComparableをconformしたRangeとClosedRangeとの区別は開区間と閉区間のイメージで、これまでの言語だったらまったく区別しなかったのにわざわざこうしたのは、位相空間での近傍の開と閉との（$\epsilon$近傍とその閉包）違いがずっとあとの収束性の議論や完備性に影響する重要な概念だからそれにならった、と言うふうにも思える。
こういうことは、Swiftを使いこなす役には立たないけど、そんなふうにしてSwiftを作ったんだ、と思うと面白い。
しかし僕が代数を思い出すのはほんとうに久しぶり。僕は院1年のときに数学の講義でかじった。学部のときに全然わからなくて試験を乗り越えるためにただ丸暗記したブラベ格子が、代数を勉強したおかげでなんとなく身近になった。入社直後に教わったCDの誤り訂正の理論も他のみんなほどの抵抗はなかった。少なくとも僕には代数構造を勉強することで、代数だけでなく解析学もわかりやすくなったような気がしていた。だからと言って数学が得意になったわけではないけど。
最初、僕はSwiftを「ようするにCとおさらばしたObjective-Cという感じ」だと思っていたけど、ちゃんと勉強を始めてみると、結構Objecitve-Cとは違っていて面白い、と思うようになってきた。単に文法をすっきりさせて流行りを取り込んだだけ、というわけではないらしい。
なんとなくわかってきたのが、LLVMの解析能力をフルに使えるような工夫がいろいろあるように思えるところ。ARCはその最たるものだし、整数や実数なんか（Cではスカラ型と分類される）までStructの仲間にしておきながら、実行時のメモリや命令のオーバーヘッドはCと変わらない、というのもできる限りコンパイル時点で解析して静的に解決するような言語仕様になっているからだろう。Objective-Cとは真逆の考え方である。
さらにProtocolの位置付けがObjective-Cとはかなり違っている、というのに気がついた。特にSwift Standard Libraryに含まれる基本的なProtocolは数学のあるものによく似ている．．．．．
Protocolは最初Objective-Cのリモートなオブジェクトとの通信のオーバーヘッドを減らすために考えられた便宜的なものらしいけど、そのうちいろんなところにProtocolを見るようになっていた。例えばNSObjectのカテゴリとして緩く宣言されていたdelegateメソッドなんかもProtocolとして「使う使わない」をはっきりとさせるようになった。
Protocolは、構造体がデータをひとまとめにしたものとみなせるように、操作をひとまとめにしたものとざっくり考えていい（と僕は思っている）が、Swiftではさらに一歩踏み込んでいる。僕の理解では、Swiftでは整数までStructだとみなしたので、プログラミングで使うあらゆるオブジェクトというか実体に対して、Protocolによって可能な操作の分類を与えることができる。
なんのことを言ってるんだかわからないけど、もう少し具体的に言えば、例えば二つの整数は大小の比較ができる。また文字列も辞書順で比べれば二つの文字列に順番を与えることができる。数学の言葉で言うと整数全体の集合も文字列全体の集合も全順序集合とみなせる。全順序なら実体が整数であろうが文字列であろうが、複数の元を一意の（常に同じ）順番で並べることができて、その方法（アルゴリズム）は整数でも文字列でも同じものが使える、ということになる。この「大小の比較可能」と言う性質をSwiftでは「Comparable」というProtocolで表す。さっきの一意の順番に整列させる操作を「ソート」と言うけど、「Comparable」Protocolをconformするオブジェクトは自動的にソートが可能になる。
「Comparable」も含めて具体的なProtocolはSwiftの言語仕様には含まれていなくて、Swift Standard Libraryの一部になっているが、その言語仕様の一部はStandard libraryが前提に（たとえばfor inループとか）なっている。
「Comparable」の他にも、基本的なProtocolとして例えばふたつの元が同じかどうかが判断できる「Equatable」、その判断のためにハッシュ値を割り当てることができる「Hashable」、ふたつの元の距離が定義できる「Strideable（なんでStridableじゃないんだろう）」など、非常に基本的なものが用意されている。
こういった仕様は（JavaやRubyとかには演算子を再定義するために現れることはあるけど）これまでのプログラミング言語ではごく当たり前の、暗黙の性質だとしてあからさまには現れてこなかった。Swiftではこういう性質の分類をProtocolをconformすることに対応させている。「Comparable」ProtocolにConformするオブジェクト（なんども書くけどクラスのインスタンスだけでなくStruct以下すべで含めて）の集合に対してはひとつのソート関数だけでいいし、「Strideable」なオブジェクトだと、それが巨大なクラスのインスタンスだったとしても、例えば配列のindexに使える、ということになる。
ただし、実際の「ふたつの元の大小を判断する」ための具体的な関数はそれぞれのオブジェクトごとに実装する必要がある。Protocolはただ「ふたつの元の大小が判断できる」という性質だけを定義して、その実装は問わない、というものである。
Swift Standard Libraryの中にそういう基本的なProtocolがいくつあってそれぞれどうなっているのか、と思ってドキュメントを見てもそれぞれの記述はあるけど全体がわかるようにはなっていない。何かないかと探していると親切な人がいた。Standfard LibraryにあるStruct、Class、EnumとProtocolの継承関係をDOT言語というグラフ記述言語で網羅してくれている。gitをcloneしてくるとその中のsslcd.dotというファイルにまとめられている。こう言うのを作ってくれているのはすごくありがたい。感謝。
僕はDOT言語を知らなかったけど見ればそれほど難しくはない。でもソースだけ眺めていても全然わからないし、このためだけにgraphvizをインストールするのもイマイチなので、いつものパターンでMathematicaに読み込んでみる。
Mathematicaはグラフを表示する機能があって、DOT言語の記述も読み込める。
In[2]:=gr = Import["sslcd.dot"];そのまま表示させると巨大な毛糸玉みたいなのができるだけなので、Protocolだけを抜き出してみる。作った人の記述によればProtocolは灰色のノードとして書かれているらしい。そこで適当な（Protocolだとわかっている）Equatableノードを探して、そのPropertyを表示してみる。
In[3]:=PropertyList[{gr, "Equatable"}]
Out[3]={"FillColor", "FixedSize", "Height", "Label", "LabelFontColor",
"LabelFontName", "LabelFontSize", "Shape", "Style", "Width",
VertexCoordinates, VertexLabels, VertexShape, VertexShapeFunction,
VertexSize, VertexStyle}
文字列になっているPropertyはDOT言語で書かれた記述にあるものだろうと考えて、"FillColor"がノードの色だろうとして
In[4]:=protocolFillColor = PropertyValue[{gr, "Equatable"}, "FillColor"];
としてとってくる。これと同じPropertyを持ったものがProtocolノードだろう。ということで
In[5]:=VertexList[gr, _?(PropertyValue[{gr, #}, "FillColor"] ==
protocolFillColor &)]
Out[5]={"UnicodeCodec", "LazyCollectionProtocol", "LazySequenceProtocol",
"IteratorProtocol", "Sequence", "AbsoluteValuable",
"BinaryFloatingPoint", "FloatingPoint", "SignedNumber", "Strideable",
"BitwiseOperations", "Integer", "SignedInteger", "UnsignedInteger",
"OptionSet", "RawRepresentable", "SetAlgebra", "TextOutputStream",
"TextOutputStreamable", "AnyObject", "Error", "MirrorPath",
"BidirectionalCollection", "CVarArg", "Collection", "Comparable",
"CustomLeafReflectable", "CustomReflectable", "Equatable",
"Hashable", "IntegerArithmetic", "LosslessStringConvertible",
"MutableCollection", "RandomAccessCollection",
"RangeReplaceableCollection", "_Incrementable"}
で、どうやら正解らしい。合計36個ある。これを見やすいグラフに表示させる。
In[7]:=LayeredGraphPlot[Subgraph[gr, VertexList[gr,
_?(PropertyValue[{gr, #}, "FillColor"] == protocolFillColor &)]], Bottom]
独立したノードもあるので、一番大きな「Equatable」Protocolを継承するものだけを取り出すと（Mathematicaの出力でも簡単に見やすくするのは難しくて、とりあえず描いてIllustratorで調整した）
ところでこのProtocolの「実装は問わずに可能な操作だけを定義する」という方針は、抽象代数に出てくる代数構造によく似ている。抽象代数では、集合の元がなんであるか、は問わずに集合が満たすべき公理を定義して、それだけから議論を展開する。例えば「群」は、集合に2項演算が定義されてその演算に関して閉じていて、その演算が結合法則を満たして、かつ単位元と逆元が存在するような集合のことである。その元は数なのか林檎なのか梨なのかそれとも別の何かなのか、その2項演算とは具体的に何をすることなのか、などということは気にしないしどうでもいい。
この群を研究する数学が群論で、たったこれだけのことから例えば5次以上の代数方程式の解の公式は作れないことが証明できたり、固体結晶の原子の並び方は（3次元では）32種類しかないことが言えたりする（ただしその証明は群の性質だけからではなくて整数の構造が反映している）。
群以外にも、群の定義のうち単位元逆元の存在しない「半群」、もっと簡単な単に2項演算が定義されているだけの「マグマ」や、逆にふたつの2項演算が定義されて、一つの演算に関してアーベル群で、もう一方がモノイドで、アーベル群の演算に対してモノイドになる演算が分配的になる、という公理を満たすものを「体」などという。体のうち元の濃度（個数）が有限のものを有限体と言って、これは誤り訂正に使われたりしている。
Wikipediaに出てくる基本的な代数構造を同じようなグラフに描いてみると
ちなみにこのグラフを書くMathematicaコード（上と同じにするには修正が必要）は
vertis = {magma, quasiGroup, loop, semigroup, monoid, group,
abelianGroup, ring, commutativeRing, integralDomain, field};
vname = {"magma", "quasi-group", "loop", "semigroup", "monoid",
"group", "abelian group", "ring", "commutative ring",
"integral domain", "field"};
vnamej = {"マグマ", "擬群", "ループ", "半群", "モノイド", "群", "アーベル群", "環",
"可換環", "整域", "体"};
alge = With[{names = vnamej},
Graph[names, {quasiGroup -> magma, loop -> quasiGroup,
loop -> magma, semigroup -> magma, monoid -> semigroup,
group -> semigroup, group -> monoid, group -> loop,
abelianGroup -> group, ring -> abelianGroup, ring -> monoid,
commutativeRing -> ring, integralDomain -> commutativeRing,
field -> ring, field -> group, field -> abelianGroup} /.
Thread[Rule[vertis, names]], VertexLabels -> "Name"]];
LayeredGraphPlot[alge, Bottom]
ちなみに、ここに書いたMathematicaコードはすべてRaspberry PiのMathematicaでも実行可能である。実行してみれば僕がどれだけIllustratorで苦労したかわかる。さらにちなみに、「_」アンダスコアがワイルドカードになったり、mapやfilterはMathematicaのMap、Selectそのままの動作だったりして、Mathematicaユーザとしては親しみやすい。こうやって代数の構造と比較してみるとSwift Standard LibraryのProtocolは公理論的だ、と言える。こういうのは単に整理がつきやすいだけでなく、ある挙動がなにに基づいているか、全然別の実体が全く同じ挙動をする原因、その挙動の本質がわかったりする。例えば量子力学のシュレーディンガー方程式とハイゼンベルク方程式が見た目は全然違うのに同じ結果を返すのは何故なのか、が理解しやすくなる。
こういう公理論的な考え方はヒルベルトがやりだして、ブルバキが徹底的にやったものらしい。Siwftを設計したひとのなかにヒルベルトのファンやブルバキのシンパがいるのだろうか。他にもComparableをconformしたRangeとClosedRangeとの区別は開区間と閉区間のイメージで、これまでの言語だったらまったく区別しなかったのにわざわざこうしたのは、位相空間での近傍の開と閉との（$\epsilon$近傍とその閉包）違いがずっとあとの収束性の議論や完備性に影響する重要な概念だからそれにならった、と言うふうにも思える。
こういうことは、Swiftを使いこなす役には立たないけど、そんなふうにしてSwiftを作ったんだ、と思うと面白い。
しかし僕が代数を思い出すのはほんとうに久しぶり。僕は院1年のときに数学の講義でかじった。学部のときに全然わからなくて試験を乗り越えるためにただ丸暗記したブラベ格子が、代数を勉強したおかげでなんとなく身近になった。入社直後に教わったCDの誤り訂正の理論も他のみんなほどの抵抗はなかった。少なくとも僕には代数構造を勉強することで、代数だけでなく解析学もわかりやすくなったような気がしていた。だからと言って数学が得意になったわけではないけど。
2018-12-15 22:12
nice!(0)
コメント(0)
コメント 0