ガウシアンビームの疑問 [ガウシアンビーム]
ガウシアンビームの話はあともう少しというところでほったらかしになっている。まあ残りはオマケみたいなのしかないのでこれで終わりとしてもいい。
そうやってガウシアンビームのことは、仕事で使うせいもあってそれなりに勉強したつもりだった。でも、ある知り合いの人からガウシアンビームに関して「こうなるのはおかしいんじゃないの？」という問題をもらって、それに答えられなかった。
しばらく考えてやっと僕なりに答えをみつけた。それが面白かったのでここに書くことにする．．．
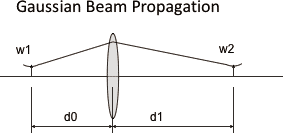ガウシアンビームを薄肉レンズに透過することを考える。この図のように、レンズから$d_0$の位置にウェストがあるガウシアンビームがレンズを透過してレンズから$d_1$の位置にウェストができているとする。
これがもし幾何光学的な結像だとすると、いわゆる「レンズの式」 \begin{equation} \frac{1}{d_0} + \frac{1}{d_1} = \frac{1}{f} \label{lensmaker} \end{equation} となるが、ガウシアンビームではもう少し複雑な \begin{equation} d_1 = \frac{\displaystyle \left(\frac{\pi w_1^2}{\lambda}\right)^2\frac{1}{f} - d_0\left(1-\frac{d_0}{f} \right)} {\displaystyle\left(\frac{\pi w_1^2}{\lambda}\right)^2 \left(\frac{1}{f} \right)^2 +\left(1-\frac{d_0}{f} \right)^2} \label{gaussianbeamlensequation} \end{equation} というふうになるという。これは幾何光学的近似として$w_1 \rightarrow 0$とすると、式-2は式-1に一致することが確かめられる。
一方、$d_0 \rightarrow f$とすると、式-2は \begin{equation} d_1 = f \label{waistrelay} \end{equation} と簡単になる。これはレンズの式からは$d_1 \rightarrow \infty$でなければならないが、これでは像側の焦点位置に結像するということになる。
現実にはこう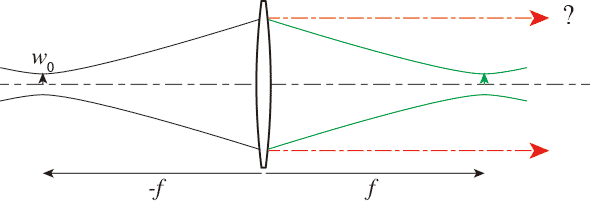
（緑線ではなく赤矢印のように）でないとおかしいんじゃないの？というわけである。
ガウシアンビームのレンズの式は近軸理論と矛盾する、という問題である。
僕がガウシアンビームをレンズに通すときは倍率の大きな場合しかなく、こう言う状況はあまりまじめに考えたことがなかった。たしかに変だ、という気がする。
ちなみに、ウェスト間の倍率$\beta$は、その2乗が \begin{equation} \beta^2 \equiv \left(\frac{w_2}{w_1} \right)^2 = \frac{1} {\displaystyle \left(\frac{\pi w_1^2}{\lambda}\right)^2 \left(\frac{1}{f} \right)^2 +\left(1-\frac{d_0}{f} \right)^2} \end{equation} となる。これは$w_1 \rightarrow 0$とすると \begin{equation} \beta = \frac{1}{\displaystyle\left(\frac{\pi w_1^2}{\lambda}\right) \left(\frac{1}{f} \right)} \end{equation} で、レンズから等距離にあるにもかかわらず等倍ではなく、ウェストのサイズに依存する、ということになる。直感とは相容れない、という気がする。
薄肉レンズによるガウシアンビームの伝播を、まえやった近軸マトリクスを使った方法で表してみる。
$w_0$のウェストから距離$d_0$の位置にある焦点距離$f$の薄肉レンズに入り、レンズから距離$d_1$の位置でウェスト$w_1$ができているとする（近軸マトリクスでは距離は$j$番目の要素から$j+1$番目の要素への方向で符号を決めるので注意）。 近軸マトリクスを使う。
$j$番目の媒質内でのガウシアンビームの複素パラメータを$q_j$ \begin{equation} q_j = \frac{z_j+ i {z_R}_j}{n_j} \end{equation} とする。$z_j$はウェストからの距離、${z_R}_j$はその媒質内でのRayleigh長さ \begin{equation} {z_R}_j = \frac{\pi w_j^2}{\lambda} \end{equation} で、$n_j$はその媒質の屈折率、$i$は虚数単位である。
$w_0$から$w_1$への伝播は、近軸マトリクスを使って \begin{align} (\hat{q}_1,\hat{p}) &= (q_0,1)\cdot \left( \begin{array}{cc} 1 & 0 \\ d_0 & 1 \end{array} \right) \cdot \left( \begin{array}{cc} 1 & -\phi \\ 0 & 1 \end{array} \right) \cdot \left( \begin{array}{cc} 1 & 0 \\ d_1 & 1 \end{array} \right) \label{pmat} \\ q_1 &= \frac{\hat{q}_1}{\hat{p}} \end{align} と書ける。ただし \begin{equation} \phi \equiv \frac{1}{f} \nonumber \end{equation} で、どちらの媒質も空気($n_0=n_1=1$）とした。
式-\ref{pmat}のマトリクスを計算してしまうと \begin{align} (\hat{q}_1,\hat{p}) &= (q_0,1)\cdot \left( \begin{array}{cc} 1 - d_1 \phi & -\phi \\ d_0+d_1(1 - d_0 \phi) & 1 - d_0 \phi \end{array} \right) \nonumber \\ &= \left( \begin{array}{cc} d_0+q_0+d_1(1-\phi (d_0+q_0)) \\ 1-\phi(d_0+q_0) \end{array} \right) \end{align} なので \begin{align} q_1 &= \frac{d_0+q_0+d_1(1-\phi(d_0+q_0))}{1-\phi(d_0+q_0)} \nonumber \\ z_1+ i {z_R}_1 &= \frac{d_0+d_1+z_0-(d_0+z_0) d_1 \phi + i \left({z_R}_0(1-d_1 \phi) \right)}{1-\phi(d_0+z_0)-i {z_R}_0} \label{q1value} \end{align} である。ここで$d_0$、$d_1$ではそれぞれのビームのウェストだとしたので \begin{equation} z_0 = z_1 = 0 \nonumber \end{equation} つまり$z_0=0$のとき式-\ref{q1value}の実部は0でなければならない。この条件で式-\ref{q1value}を$d_1$に関して解くと \begin{equation} d_1 = \frac{{z_R}_0^2 \phi - d_0 (1-d_0 \phi)}{{z_R}_0^2 \phi^2+(1-d_0 \phi)^2} \label{result0} \end{equation} となって式-\ref{gaussianbeamlensequation}をRayleigh長さなどに書き換えたものに一致する。従って式-\ref{gaussianbeamlensequation}は近軸マトリクスを使った計算と等価である。
う〜ん、おかしいな。
同じようにしてこの場合の$d_1$を計算すると \begin{align} d_1 &= \frac{2+\phi^2 {z_R}_0^2}{\phi(1+\phi^2 {z_R}_0^2)} \\ &= \frac{f(2f^2+{z_R}_0^2)}{f^2+{z_R}_0^2} \nonumber \end{align} となる。さらに \begin{align} {z_R}_1 &= \frac{{z_R}_0}{1+(\phi {z_R}_0)^2} \\ &= \frac{f^2 {z_R}_0}{f^2+{z_R}_0^2} \end{align} となって、${z_R}_0 \ll f$とするとどちらも等倍の関係（$d_1 \approx 2f,{z_R}_1 \approx {z_R}_0$）に近くなる。
こっちのほうはもっともらしい。
近軸波動方程式は、自由空間のスカラの波動方程式に$z$方向の場の依存性はゆっくりだ、とした近似を入れて導いたものだった。
$z$軸を対称軸にするガウシアンビームにはこの図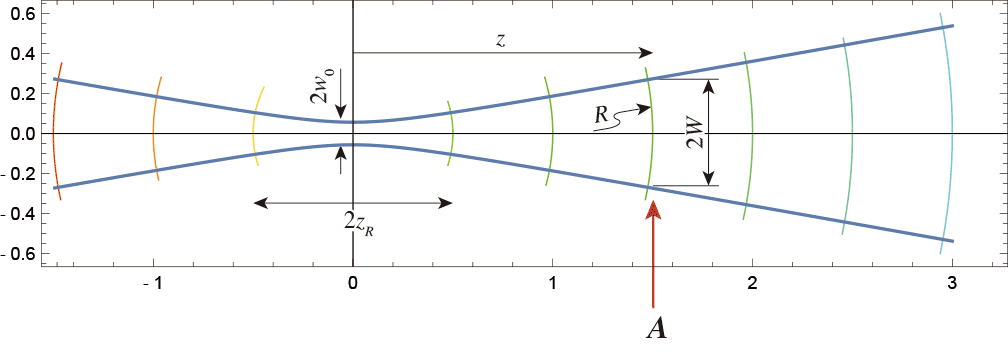
のような特徴量がいくつかある。ビームそのものは波長$\lambda$とRayleigh長さ$z_R$で一意に指定できる。そして例えば図中の$A$の位置の場は、さらにウェストからの距離$z$を指定することで完全に決定できる。$z$方向の場の依存性はゆっくりだという条件が入っているので、$z_R \gg \lambda$が成り立つときだけ正しい。
そのガウシアンビームのウェスト幅$w$は \begin{equation} w = \sqrt{\frac{\lambda z_R}{\pi}} \label{waist} \end{equation} そのウェストからの距離$z$の位置での半径$W(z)$は \begin{equation} W(z) = \sqrt{\frac{\lambda}{\pi}\frac{z^2+z_R^2}{z_R}} \label{beamradius} \end{equation} その位置での波面（場の等位相面）の曲率半径$R(z)$は \begin{equation} R(z) = z+\frac{z_R^2}{z} \end{equation} である。$R(z)$は近軸波動方程式の解の形によるもので、波面が$z$の正の方向に凸の場合（ウェストから正の方向に離れた位置）に正の値になる。
ところで、うっかり間違って波面の曲率半径の符号の取り方をこの式のままで最後まで計算してしまった。普通の人はこの符号の取り方をするのでいいんだけど、僕が前書いたのとか光線追跡での定義などとは逆になってしまう。昔こっちがいい、と主張して自分で符号をひっくり返して定式化したくせにそれを忘れて無視するというのは情けない。皆さんもお気をつけください。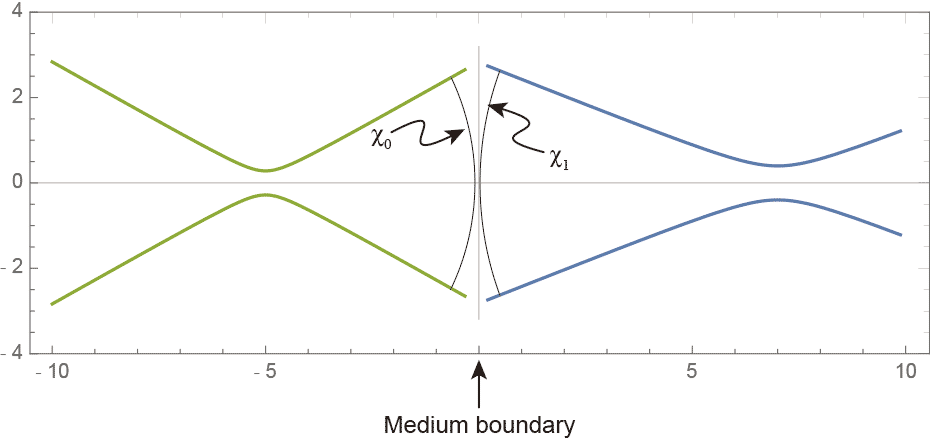
のような厚さ0のレンズによるガウシアンビームの変換を考える。
ガウシアンビームは波動方程式から導びかれた解なので、幾何光学的な考え方とは相性がよくない。従って、レンズも光線を屈折させる部品ではなく、波面、つまり電場の等位相面の曲率を変換する素子だと考えないといけない。
Abbeの不変式から、レンズの屈折力を$\phi$としたとき近軸の範囲では、波面の曲率$\chi =1/R(z)$は \begin{equation} \chi_1 = \chi_0 - \phi \label{curvature} \end{equation} と変換されると考えていい。ただし、曲率の符号は$R(z)$のとりかたと同じだとする。
薄肉レンズは平面でその裏表（入射前と射出後）でのビーム半径$W(z)$は変わらない。したがってレンズによってガウシアンビームのパラメータが$(z_0,z_{R0})$から$(z_1,z_{R1})$に変換されると考える。
レンズの位置を$z=0$にとり、レンズの左右の領域にそれぞれガウシアンビームのウェストがあってレンズからの距離がそれぞれ$z_0$と$z_1$（$z_0 \lt 0 \lt z_1$）とする。
波面の曲率の変換の式-\ref{curvature}から \begin{equation} \frac{1}{R_1(z_1)} = \frac{1}{R_2(z_0)} - \phi \label{wavefrontcurvature} \end{equation} であり、ビーム半径から \begin{equation} W_1(z_1) = W_0(z_0) \end{equation} である。このふたつの式を連立させて$(z_1,z_{R1})$を$(z_0,z_{R0})$で表せばレンズによるガウシアンビームの変換が直接書き下せることになる。
具体的に書くと \begin{align} \frac{z_1}{z_1^2+z_{R1}^2} &= \frac{z_0}{z_0^2+z_{R0}^2} -\phi \nonumber \\ \frac{z_1^2+z_{R1}^2}{z_{R1}} &= \frac{z_0^2+z_{R0}^2}{z_{R0}} \nonumber \end{align} と、よく似てるけど微妙に違う式になる。ただしここで$\lambda>0$と$z_R>0$として平方根を開いた。2番目の式は$z_R$は0にはならないので \begin{equation} \frac{z_{R1}}{z_1^2+z_{R1}^2} = \frac{z_{R0}}{z_0^2+z_{R0}^2} \nonumber \end{equation} とすると分母は同じになる。
これらを連立させて解くと（というか、Mathematicaに解かせると） \begin{equation} \left\{ \begin{array}{rl} \displaystyle z_1 =& \frac{\displaystyle z_0-\left(z_0^2+z_{R0}^2 \right)\phi }{\displaystyle 1-2z_0\phi +\left(z_0^2+z_{R0}^2 \right)\phi^2} \\ \displaystyle z_{R1} =& \frac{\displaystyle z_{R0}}{\displaystyle 1-2z_0\phi +\left(z_0^2+z_{R0}^2 \right)\phi^2} \end{array} \right. \label{exactresult0} \end{equation} となる。結果の分母は同じである。$z_0$を$d_0$と置き換えると式-\ref{result0}と一致する。したがって近軸マトリクスによる計算はこれと完全に等価だということになる。思い出せば、もっと一般的に等価性を証明した記憶があるな。改めて昔書いたのを見て「そりゃそうだな」と思った。全く無駄なことをした。いまさらだけど。
そして例の条件$z_0 \rightarrow 1/\phi$とすると（符号に注意。$z_j$は媒質$j$のウェスト位置から測っている） \begin{align} z_1 &= -\frac{1}{\phi} \nonumber \\ z_{R1} &= \frac{1}{z_{R0}\phi^2} \label{rayleighlengthofimage} \end{align} となって、$z_1$に関しては当然同じ結論になる。
しかしこれでは確認ができただけで、話は進んでいない。次回この先を考えることにする。
そうやってガウシアンビームのことは、仕事で使うせいもあってそれなりに勉強したつもりだった。でも、ある知り合いの人からガウシアンビームに関して「こうなるのはおかしいんじゃないの？」という問題をもらって、それに答えられなかった。
しばらく考えてやっと僕なりに答えをみつけた。それが面白かったのでここに書くことにする．．．
1 その問題とは
その問題提起というのはこうである。こんな図をもらった。これがもし幾何光学的な結像だとすると、いわゆる「レンズの式」 \begin{equation} \frac{1}{d_0} + \frac{1}{d_1} = \frac{1}{f} \label{lensmaker} \end{equation} となるが、ガウシアンビームではもう少し複雑な \begin{equation} d_1 = \frac{\displaystyle \left(\frac{\pi w_1^2}{\lambda}\right)^2\frac{1}{f} - d_0\left(1-\frac{d_0}{f} \right)} {\displaystyle\left(\frac{\pi w_1^2}{\lambda}\right)^2 \left(\frac{1}{f} \right)^2 +\left(1-\frac{d_0}{f} \right)^2} \label{gaussianbeamlensequation} \end{equation} というふうになるという。これは幾何光学的近似として$w_1 \rightarrow 0$とすると、式-2は式-1に一致することが確かめられる。
一方、$d_0 \rightarrow f$とすると、式-2は \begin{equation} d_1 = f \label{waistrelay} \end{equation} と簡単になる。これはレンズの式からは$d_1 \rightarrow \infty$でなければならないが、これでは像側の焦点位置に結像するということになる。
現実にはこう
ガウシアンビームのレンズの式は近軸理論と矛盾する、という問題である。
僕がガウシアンビームをレンズに通すときは倍率の大きな場合しかなく、こう言う状況はあまりまじめに考えたことがなかった。たしかに変だ、という気がする。
ちなみに、ウェスト間の倍率$\beta$は、その2乗が \begin{equation} \beta^2 \equiv \left(\frac{w_2}{w_1} \right)^2 = \frac{1} {\displaystyle \left(\frac{\pi w_1^2}{\lambda}\right)^2 \left(\frac{1}{f} \right)^2 +\left(1-\frac{d_0}{f} \right)^2} \end{equation} となる。これは$w_1 \rightarrow 0$とすると \begin{equation} \beta = \frac{1}{\displaystyle\left(\frac{\pi w_1^2}{\lambda}\right) \left(\frac{1}{f} \right)} \end{equation} で、レンズから等距離にあるにもかかわらず等倍ではなく、ウェストのサイズに依存する、ということになる。直感とは相容れない、という気がする。
2 近軸マトリクスによる導出
まず、最初の式-2が正しいのか確認する。薄肉レンズによるガウシアンビームの伝播を、まえやった近軸マトリクスを使った方法で表してみる。
$w_0$のウェストから距離$d_0$の位置にある焦点距離$f$の薄肉レンズに入り、レンズから距離$d_1$の位置でウェスト$w_1$ができているとする（近軸マトリクスでは距離は$j$番目の要素から$j+1$番目の要素への方向で符号を決めるので注意）。 近軸マトリクスを使う。
$j$番目の媒質内でのガウシアンビームの複素パラメータを$q_j$ \begin{equation} q_j = \frac{z_j+ i {z_R}_j}{n_j} \end{equation} とする。$z_j$はウェストからの距離、${z_R}_j$はその媒質内でのRayleigh長さ \begin{equation} {z_R}_j = \frac{\pi w_j^2}{\lambda} \end{equation} で、$n_j$はその媒質の屈折率、$i$は虚数単位である。
$w_0$から$w_1$への伝播は、近軸マトリクスを使って \begin{align} (\hat{q}_1,\hat{p}) &= (q_0,1)\cdot \left( \begin{array}{cc} 1 & 0 \\ d_0 & 1 \end{array} \right) \cdot \left( \begin{array}{cc} 1 & -\phi \\ 0 & 1 \end{array} \right) \cdot \left( \begin{array}{cc} 1 & 0 \\ d_1 & 1 \end{array} \right) \label{pmat} \\ q_1 &= \frac{\hat{q}_1}{\hat{p}} \end{align} と書ける。ただし \begin{equation} \phi \equiv \frac{1}{f} \nonumber \end{equation} で、どちらの媒質も空気($n_0=n_1=1$）とした。
式-\ref{pmat}のマトリクスを計算してしまうと \begin{align} (\hat{q}_1,\hat{p}) &= (q_0,1)\cdot \left( \begin{array}{cc} 1 - d_1 \phi & -\phi \\ d_0+d_1(1 - d_0 \phi) & 1 - d_0 \phi \end{array} \right) \nonumber \\ &= \left( \begin{array}{cc} d_0+q_0+d_1(1-\phi (d_0+q_0)) \\ 1-\phi(d_0+q_0) \end{array} \right) \end{align} なので \begin{align} q_1 &= \frac{d_0+q_0+d_1(1-\phi(d_0+q_0))}{1-\phi(d_0+q_0)} \nonumber \\ z_1+ i {z_R}_1 &= \frac{d_0+d_1+z_0-(d_0+z_0) d_1 \phi + i \left({z_R}_0(1-d_1 \phi) \right)}{1-\phi(d_0+z_0)-i {z_R}_0} \label{q1value} \end{align} である。ここで$d_0$、$d_1$ではそれぞれのビームのウェストだとしたので \begin{equation} z_0 = z_1 = 0 \nonumber \end{equation} つまり$z_0=0$のとき式-\ref{q1value}の実部は0でなければならない。この条件で式-\ref{q1value}を$d_1$に関して解くと \begin{equation} d_1 = \frac{{z_R}_0^2 \phi - d_0 (1-d_0 \phi)}{{z_R}_0^2 \phi^2+(1-d_0 \phi)^2} \label{result0} \end{equation} となって式-\ref{gaussianbeamlensequation}をRayleigh長さなどに書き換えたものに一致する。従って式-\ref{gaussianbeamlensequation}は近軸マトリクスを使った計算と等価である。
う〜ん、おかしいな。
2.1 普通の等倍結像の場合
$d_0 = 2f$の場合を考えてみる。この場合近軸理論では像点は$d_1=2f$の位置になるはずである。同じようにしてこの場合の$d_1$を計算すると \begin{align} d_1 &= \frac{2+\phi^2 {z_R}_0^2}{\phi(1+\phi^2 {z_R}_0^2)} \\ &= \frac{f(2f^2+{z_R}_0^2)}{f^2+{z_R}_0^2} \nonumber \end{align} となる。さらに \begin{align} {z_R}_1 &= \frac{{z_R}_0}{1+(\phi {z_R}_0)^2} \\ &= \frac{f^2 {z_R}_0}{f^2+{z_R}_0^2} \end{align} となって、${z_R}_0 \ll f$とするとどちらも等倍の関係（$d_1 \approx 2f,{z_R}_1 \approx {z_R}_0$）に近くなる。
こっちのほうはもっともらしい。
3 もっとはじめの方から導く
自分ではほとんど使わないせいもあって、近軸マトリクスによる式は、なんでこれでいけるのかピンとこないという感じが昔からずっとしている。それは計算の方便であって実はどこかに制約があるのではないか、つまり、広い範囲ではあるけどある特定の条件でだけ成り立つのではないか、と思ったので、近軸波動方程式の解としてのガウシアンビームの式まで戻って考えることにした。近軸波動方程式は、自由空間のスカラの波動方程式に$z$方向の場の依存性はゆっくりだ、とした近似を入れて導いたものだった。
$z$軸を対称軸にするガウシアンビームにはこの図
そのガウシアンビームのウェスト幅$w$は \begin{equation} w = \sqrt{\frac{\lambda z_R}{\pi}} \label{waist} \end{equation} そのウェストからの距離$z$の位置での半径$W(z)$は \begin{equation} W(z) = \sqrt{\frac{\lambda}{\pi}\frac{z^2+z_R^2}{z_R}} \label{beamradius} \end{equation} その位置での波面（場の等位相面）の曲率半径$R(z)$は \begin{equation} R(z) = z+\frac{z_R^2}{z} \end{equation} である。$R(z)$は近軸波動方程式の解の形によるもので、波面が$z$の正の方向に凸の場合（ウェストから正の方向に離れた位置）に正の値になる。
ところで、うっかり間違って波面の曲率半径の符号の取り方をこの式のままで最後まで計算してしまった。普通の人はこの符号の取り方をするのでいいんだけど、僕が前書いたのとか光線追跡での定義などとは逆になってしまう。昔こっちがいい、と主張して自分で符号をひっくり返して定式化したくせにそれを忘れて無視するというのは情けない。皆さんもお気をつけください。
3.1 薄肉レンズによるガウシアンビームの変換
この図ガウシアンビームは波動方程式から導びかれた解なので、幾何光学的な考え方とは相性がよくない。従って、レンズも光線を屈折させる部品ではなく、波面、つまり電場の等位相面の曲率を変換する素子だと考えないといけない。
Abbeの不変式から、レンズの屈折力を$\phi$としたとき近軸の範囲では、波面の曲率$\chi =1/R(z)$は \begin{equation} \chi_1 = \chi_0 - \phi \label{curvature} \end{equation} と変換されると考えていい。ただし、曲率の符号は$R(z)$のとりかたと同じだとする。
薄肉レンズは平面でその裏表（入射前と射出後）でのビーム半径$W(z)$は変わらない。したがってレンズによってガウシアンビームのパラメータが$(z_0,z_{R0})$から$(z_1,z_{R1})$に変換されると考える。
レンズの位置を$z=0$にとり、レンズの左右の領域にそれぞれガウシアンビームのウェストがあってレンズからの距離がそれぞれ$z_0$と$z_1$（$z_0 \lt 0 \lt z_1$）とする。
波面の曲率の変換の式-\ref{curvature}から \begin{equation} \frac{1}{R_1(z_1)} = \frac{1}{R_2(z_0)} - \phi \label{wavefrontcurvature} \end{equation} であり、ビーム半径から \begin{equation} W_1(z_1) = W_0(z_0) \end{equation} である。このふたつの式を連立させて$(z_1,z_{R1})$を$(z_0,z_{R0})$で表せばレンズによるガウシアンビームの変換が直接書き下せることになる。
具体的に書くと \begin{align} \frac{z_1}{z_1^2+z_{R1}^2} &= \frac{z_0}{z_0^2+z_{R0}^2} -\phi \nonumber \\ \frac{z_1^2+z_{R1}^2}{z_{R1}} &= \frac{z_0^2+z_{R0}^2}{z_{R0}} \nonumber \end{align} と、よく似てるけど微妙に違う式になる。ただしここで$\lambda>0$と$z_R>0$として平方根を開いた。2番目の式は$z_R$は0にはならないので \begin{equation} \frac{z_{R1}}{z_1^2+z_{R1}^2} = \frac{z_{R0}}{z_0^2+z_{R0}^2} \nonumber \end{equation} とすると分母は同じになる。
これらを連立させて解くと（というか、Mathematicaに解かせると） \begin{equation} \left\{ \begin{array}{rl} \displaystyle z_1 =& \frac{\displaystyle z_0-\left(z_0^2+z_{R0}^2 \right)\phi }{\displaystyle 1-2z_0\phi +\left(z_0^2+z_{R0}^2 \right)\phi^2} \\ \displaystyle z_{R1} =& \frac{\displaystyle z_{R0}}{\displaystyle 1-2z_0\phi +\left(z_0^2+z_{R0}^2 \right)\phi^2} \end{array} \right. \label{exactresult0} \end{equation} となる。結果の分母は同じである。$z_0$を$d_0$と置き換えると式-\ref{result0}と一致する。したがって近軸マトリクスによる計算はこれと完全に等価だということになる。思い出せば、もっと一般的に等価性を証明した記憶があるな。改めて昔書いたのを見て「そりゃそうだな」と思った。全く無駄なことをした。いまさらだけど。
そして例の条件$z_0 \rightarrow 1/\phi$とすると（符号に注意。$z_j$は媒質$j$のウェスト位置から測っている） \begin{align} z_1 &= -\frac{1}{\phi} \nonumber \\ z_{R1} &= \frac{1}{z_{R0}\phi^2} \label{rayleighlengthofimage} \end{align} となって、$z_1$に関しては当然同じ結論になる。
しかしこれでは確認ができただけで、話は進んでいない。次回この先を考えることにする。
2019-08-10 20:56
nice!(0)
コメント(0)
コメント 0