NBodySimulation関数で遊ぶ [日常のあれやこれや]
デスクトップ版と一緒にRaspberry Pi用(pi4+busterでは最初コケてたけど、どうやら動くようになったらしい)のもMathematicaがバージョン12になって、また新しい関数が増えてる。僕は実質的にせいぜいバージョン6ぐらいの時点での機能しか使ってなくて、それ以降に導入された機能はたまにみつけて「ああ、こんなのがあるんだ」と思うぐらいでしかない。でももったいないのでバージョンが上がるといちおうどんなのが増えたのか確認だけはしている....
Aroundは面白い機能でトレランス計算を簡単に表現できるかもしれない。けどなかなか使うのは難しい。でも、12の前に導入されたブロックチェインやニューラルネットなんかなんでわざわざMathematicaでやらなきゃいけないのかわからないし、12で導入されたUnityインターフェイスの膨大な量の関数は、ほんとに何に使うの?という印象しかない(でもサンプルはUnityをインストールして遊んでしまった。やっぱりぬるぬる動くとそれだけで楽しい)。
Python+Jupyter+NumPy+SymPy+SciPy+etc..で同じことができるようになってきてるうえに、Pythonのライブラリはオープンソースにありがちなごちゃごちゃ感がなくてシンプルなので、Mathematicaとしては逃げていくしかないんだろうけど。
12で導入されたNBodySimulationという関数がある。これは初期的な位置と速度ベクトルを指定するだけで、いわゆる古典論の多体問題の解を計算するというもの。とうぜんこの関数の中では微分方程式を数値積分してるはずで、もともとMathematicaが持ってる機能をつなぎ合わせただけの特定問題向けユーティリティ関数に過ぎない。しかし、多体問題の解を自分で簡単に探せるのでついつい面白くなってしまう。
NBodySimulationは
第2引数は質点や電荷を連想の形で指定した配列で、最後の引数はどのくらいの時間追跡するかを指定する。この連想は最近(といってもバージョン10で)追加されたもので、Objective-Cその他の辞書である。僕なんかはRuleの配列でいいじゃん、と思うんだけど、ハッシュつきらしくて数が増えると効率的らしい。そのかわりキーには文字列を使うか、シンボルの場合はKey[Symbol]としないといけない(仕様上は文字列ならKeyを省略可という位置付けのようである)。ああ、煩わしい。
MathematicaではEntityを導入したあたりから、関数名にならずに単に情報を保持するだけのオブジェクトにはシンボルを使わずに文字列を使うようになってきた。たぶんシンボルが増えすぎると効率の問題と、お互いを区別するためにシンボル名が長くなってしまうとか、間違って値が与えられて評価で置き換わってしまうとかいう問題があるからだろうか。しかし文字列の場合、実行しないと正しいかどうかわからなくて、ようするになんでもセマンティクスの問題になってしまって、デバグがしづらい。シンボルであってもMathematicaの場合大して違わないとは言えるんだけど。
まあそれはいいとして、多体問題を手軽に試してみることができるので、やってみた。まず2次元で質点を適当に用意する。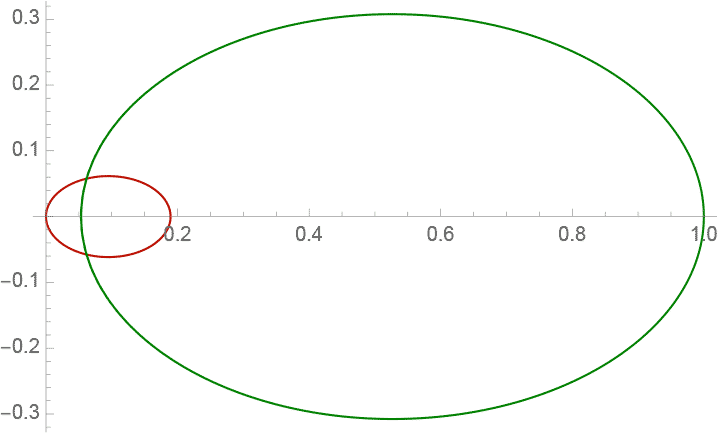 みたいになる。
みたいになる。
ムービーにするには、たとえば
質点を3つ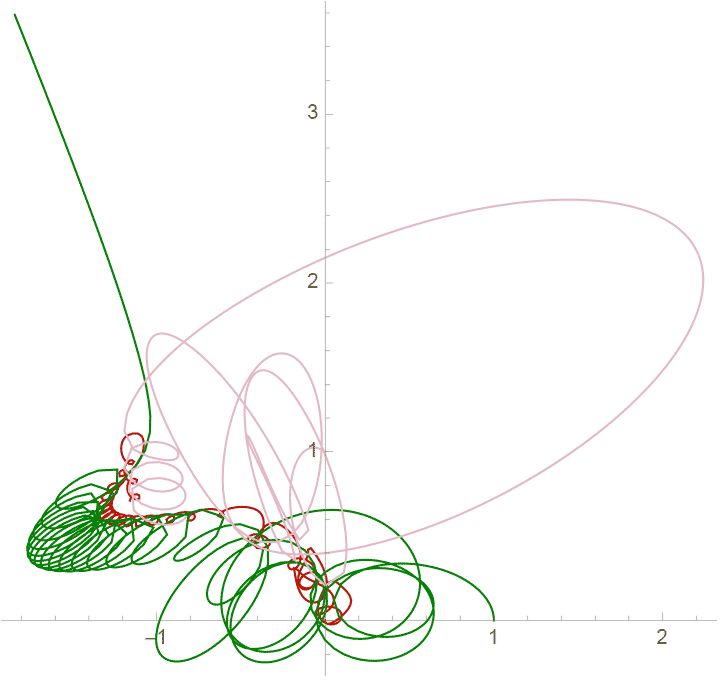 この緑の軌道はこのあと左上の方向にどんどん離れていく。
この緑の軌道はこのあと左上の方向にどんどん離れていく。
ポアンカレさんは3体問題でスリングショットしない条件を探そうとして、一般解がないことや、特殊な条件での安定解を見つけたりしたらしい。計算機のなかった時代に軌道を思い描くことができた、というのは驚きだけど、僕らは簡単にできて、ちょっとパラメータを変えるだけで軌道が全然変わることを簡単に確かめることができる。
NBodySimulationは内部で精度の評価をやってないらしくて、追跡時間の長さを変えるだけで軌道が変わってしまう。まあ、カオスに対しては数値積分ではどんな初期値に対してもいずれは精度がたりなくなるので、潔くあきらめた、ということだろう。
同じように3次元でもやってみると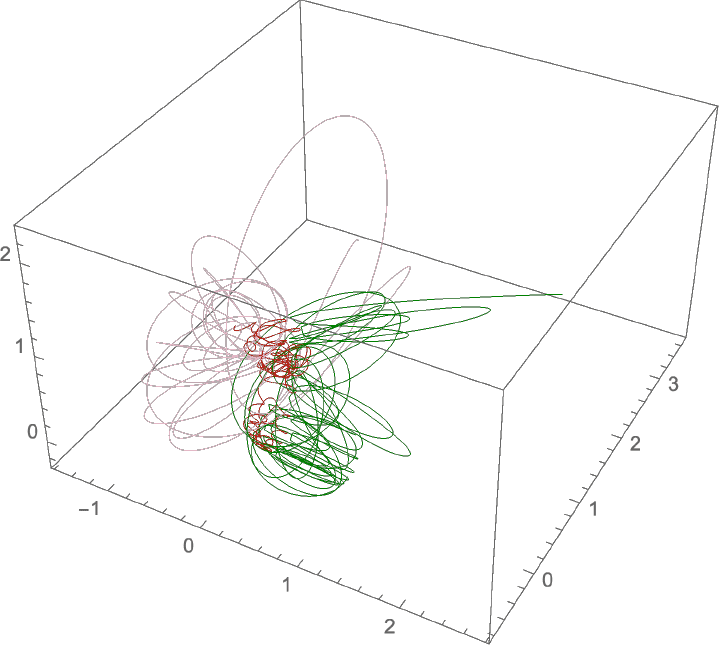 みたいになる。これも緑の軌道はこのあと右方向にスリングショットされる。
みたいになる。これも緑の軌道はこのあと右方向にスリングショットされる。
このMathemaitcaノートブックはDropboxのダウンロード先にあるので、試してみてほしい(Dropboxは例の無料アカウントの仕様変更のせいで、僕は全部他のオンラインストレージに引っ越して、今ではただの物置になってしまった。使いやすかったので残念である)。Raspberry PiのMathematicaでも3B+なら軌道を描くのは全然問題ない。でもListAnimateのムービーはちょっとずつにしないとFrontEndがメモリを使い果たしてクラッシュする。Raspberry PiのMathematicaで静止画の画像ファイルを一枚ずつ作って、パソコンで(macOSならiMovieとかで)ムービーに変換する、とかいうやりかたにすればクラッシュせずに済む。めんどくさいけど。
質点の質量、初期的な位置と速度をランダムにして走らせてみると、たいていすぐスリングショットしてしまう。質点のうち一つだけ質量を大きくするとカオスが安定になりやすいということがわかる。また、質点の数を増やしていくと、たいていはひとつずつスリングショットするけど、たまにふたつのペアで飛び出したりする。ほとんどはシューベルト的にひとりで放浪の旅に出るんだけど、ときどき駆け落ちする奴らがでてくる。$N \ge 3$でスリングショットしない安定な解を見つけるのは難しい。長時間でも計算はできるんだけど、どんどん精度が確保できなくなって解として急速に怪しくなってくる。また$N=10$ぐらいが限界で、結果が返ってもどこまで精度があるのかぜんぜんわからなくて、見るからにおかしな軌道になったりする。
ところでどんな方程式を解いているか、というと
$N \le 3$で2次元と3次元の例をムービーにした。
今の太陽系は多体系だけど、惑星がそれぞれ円に近い軌道を回っていてかなり安定に見えるが、なんでそうなったのか。NBodySimulationで遊んでいると、その理由がわかるような気がしてきた。ひとつは太陽という極端に質量の大きい天体があるのと、太陽系が形成された初期には多くの天体がスリングショットしてしまって、近似的に自身と太陽との2体問題的な軌道にある天体だけが生き残った結果ではないか、と思える。逆回りや楕円率の大きな天体は何億回と太陽の周りを回るうちに他の天体と近づきすぎてスリングショットする機会が増えて太陽系内にいなくなってしまうんだろう。
NBodySimulation関数はほんとうに単なるおもちゃでしかないけど、ポアンカレさんが人類で初めてカオスの深淵を覗いたときの感慨をちょっとだけでも味あわせてくれて、楽しい。少しの違いで軌道が全然変わってしまうのをみてるとついつい時間を忘れてしまう。MathematicaのライセンスかあるいはRaspberry Piを持っている人は遊んでみて欲しい。
僕が無意識にカオスに惹かれる遠因のひとつは、やっぱり生物として文字通りカオスから生まれてきたからだろうな。面白いな。
Aroundは面白い機能でトレランス計算を簡単に表現できるかもしれない。けどなかなか使うのは難しい。でも、12の前に導入されたブロックチェインやニューラルネットなんかなんでわざわざMathematicaでやらなきゃいけないのかわからないし、12で導入されたUnityインターフェイスの膨大な量の関数は、ほんとに何に使うの?という印象しかない(でもサンプルはUnityをインストールして遊んでしまった。やっぱりぬるぬる動くとそれだけで楽しい)。
Python+Jupyter+NumPy+SymPy+SciPy+etc..で同じことができるようになってきてるうえに、Pythonのライブラリはオープンソースにありがちなごちゃごちゃ感がなくてシンプルなので、Mathematicaとしては逃げていくしかないんだろうけど。
12で導入されたNBodySimulationという関数がある。これは初期的な位置と速度ベクトルを指定するだけで、いわゆる古典論の多体問題の解を計算するというもの。とうぜんこの関数の中では微分方程式を数値積分してるはずで、もともとMathematicaが持ってる機能をつなぎ合わせただけの特定問題向けユーティリティ関数に過ぎない。しかし、多体問題の解を自分で簡単に探せるのでついつい面白くなってしまう。
NBodySimulationは
NBodySimulation[law,{state1,…,staten},t]
として呼ぶと、解を計算してNBodySimulationDataというラッパオブジェクトを返すようになっている。第1引数の「law」は
- InverseSquare
- Harmonic
- その他
第2引数は質点や電荷を連想の形で指定した配列で、最後の引数はどのくらいの時間追跡するかを指定する。この連想は最近(といってもバージョン10で)追加されたもので、Objective-Cその他の辞書である。僕なんかはRuleの配列でいいじゃん、と思うんだけど、ハッシュつきらしくて数が増えると効率的らしい。そのかわりキーには文字列を使うか、シンボルの場合はKey[Symbol]としないといけない(仕様上は文字列ならKeyを省略可という位置付けのようである)。ああ、煩わしい。
MathematicaではEntityを導入したあたりから、関数名にならずに単に情報を保持するだけのオブジェクトにはシンボルを使わずに文字列を使うようになってきた。たぶんシンボルが増えすぎると効率の問題と、お互いを区別するためにシンボル名が長くなってしまうとか、間違って値が与えられて評価で置き換わってしまうとかいう問題があるからだろうか。しかし文字列の場合、実行しないと正しいかどうかわからなくて、ようするになんでもセマンティクスの問題になってしまって、デバグがしづらい。シンボルであってもMathematicaの場合大して違わないとは言えるんだけど。
まあそれはいいとして、多体問題を手軽に試してみることができるので、やってみた。まず2次元で質点を適当に用意する。
b1 = <|"Mass" -> 5, "Position" -> {0, 0}, "Velocity" -> {0, -0.2}|>;
b2 = <|"Mass" -> 1, "Position" -> {1, 0}, "Velocity" -> {0., 1}|>;
b3 = <|"Mass" -> 1, "Position" -> {0, 1}, "Velocity" -> {-0.7, 0.5}|>;
b4 = <|"Mass" -> 1, "Position" -> {1, 1}, "Velocity" -> {0.9, 0.2}|>;
b5 = <|"Mass" -> 1, "Position" -> {-1, 0}, "Velocity" -> {-1, 0}|>;
それぞれ質量と、初期的な位置と速度を与える。それと適当に時間方向の定数
dur = 2; tick = dur/200;を決めてとりあえずまず2体
bodies = {b1, b2};
で、
data = NBodySimulation["InverseSquare", bodies, dur];としてみる。これで逆2乗法則に従った2体問題を2単位時間追跡するということになる。返されたdataにはNDSolveと同じ時刻に対する位置の補間関数InterpolationFunctionが含まれていて、単に軌道を描くだけなら
Plot[Evaluate[data[All, "Position", t]], {t, 0, dur}]
で描くことができる。2体ではおなじみの楕円軌道で、

ムービーにするには、たとえば
pos = Table[Evaluate[data[All, "Position", t]], {t, 0, dur, tick}];
radius = Max[Map[Apply[Subtract, Reverse[#]] &, CoordinateBounds[pos]]]*0.01;
bnds = CoordinateBounds[pos, 2 radius];
glist = Map[Graphics[disks[#, radius], PlotRange -> bnds, Axes -> True] &, pos];
ListAnimate[glist]
とすると質点のアニメーションを見ることができる。中で使われているユーティリティ関数は
colorIndex = 58;
indexedColor[n_] := ColorData[colorIndex][n]
disks[lis_, r_] :=
With[{n = Length[lis]}, MapIndexed[{Apply[indexedColor, #2], Disk[#1, r]} &, lis]]
のようなものである。
質点を3つ
bodies = {b1, b2, b3};
にして同じことをすると、こんどはカオス様になって、ある時刻で一つの質点がスリングショット、つまりボイジャーのように重力に打ち勝って永遠に離れる軌道に乗る。

ポアンカレさんは3体問題でスリングショットしない条件を探そうとして、一般解がないことや、特殊な条件での安定解を見つけたりしたらしい。計算機のなかった時代に軌道を思い描くことができた、というのは驚きだけど、僕らは簡単にできて、ちょっとパラメータを変えるだけで軌道が全然変わることを簡単に確かめることができる。
NBodySimulationは内部で精度の評価をやってないらしくて、追跡時間の長さを変えるだけで軌道が変わってしまう。まあ、カオスに対しては数値積分ではどんな初期値に対してもいずれは精度がたりなくなるので、潔くあきらめた、ということだろう。
同じように3次元でもやってみると
b3D1 = <|"Mass" -> 5, "Position" -> {0, 0, 0}, "Velocity" -> {0, 0.2, 0.1}|>;
b3D2 = <|"Mass" -> 1, "Position" -> {1, 0, 0}, "Velocity" -> {0., -1, -0.5}|>;
b3D3 = <|"Mass" -> 1, "Position" -> {0, 2, 1}, "Velocity" -> {0, 0, 0.2}|>;
dur3D = 36;
tick3D = dur3D/3000;
bodies3D = {b3D1, b3D2, b3D3};
data3D = NBodySimulation["InverseSquare", bodies3D, dur3D];
で軌道を描いてみると

このMathemaitcaノートブックはDropboxのダウンロード先にあるので、試してみてほしい(Dropboxは例の無料アカウントの仕様変更のせいで、僕は全部他のオンラインストレージに引っ越して、今ではただの物置になってしまった。使いやすかったので残念である)。Raspberry PiのMathematicaでも3B+なら軌道を描くのは全然問題ない。でもListAnimateのムービーはちょっとずつにしないとFrontEndがメモリを使い果たしてクラッシュする。Raspberry PiのMathematicaで静止画の画像ファイルを一枚ずつ作って、パソコンで(macOSならiMovieとかで)ムービーに変換する、とかいうやりかたにすればクラッシュせずに済む。めんどくさいけど。
質点の質量、初期的な位置と速度をランダムにして走らせてみると、たいていすぐスリングショットしてしまう。質点のうち一つだけ質量を大きくするとカオスが安定になりやすいということがわかる。また、質点の数を増やしていくと、たいていはひとつずつスリングショットするけど、たまにふたつのペアで飛び出したりする。ほとんどはシューベルト的にひとりで放浪の旅に出るんだけど、ときどき駆け落ちする奴らがでてくる。$N \ge 3$でスリングショットしない安定な解を見つけるのは難しい。長時間でも計算はできるんだけど、どんどん精度が確保できなくなって解として急速に怪しくなってくる。また$N=10$ぐらいが限界で、結果が返ってもどこまで精度があるのかぜんぜんわからなくて、見るからにおかしな軌道になったりする。
ところでどんな方程式を解いているか、というと
data["Equations"]としてみればわかる。見れば当たり前なんだけど、$N$体問題では$N$個の2階微分方程式で、それぞれは$N-1$個の項を含んでいる。方程式は自動的に作ることができるけど、すべての項が非線形なので解の見通しはものすごく悪い。ポアンカレさんはどうやって頭の中に描いたんだろう。すごいなあ。僕はポアンカレさんのこう言うセンスの百分の一でも欲しいと憧れてしまう。
$N \le 3$で2次元と3次元の例をムービーにした。
今の太陽系は多体系だけど、惑星がそれぞれ円に近い軌道を回っていてかなり安定に見えるが、なんでそうなったのか。NBodySimulationで遊んでいると、その理由がわかるような気がしてきた。ひとつは太陽という極端に質量の大きい天体があるのと、太陽系が形成された初期には多くの天体がスリングショットしてしまって、近似的に自身と太陽との2体問題的な軌道にある天体だけが生き残った結果ではないか、と思える。逆回りや楕円率の大きな天体は何億回と太陽の周りを回るうちに他の天体と近づきすぎてスリングショットする機会が増えて太陽系内にいなくなってしまうんだろう。
NBodySimulation関数はほんとうに単なるおもちゃでしかないけど、ポアンカレさんが人類で初めてカオスの深淵を覗いたときの感慨をちょっとだけでも味あわせてくれて、楽しい。少しの違いで軌道が全然変わってしまうのをみてるとついつい時間を忘れてしまう。MathematicaのライセンスかあるいはRaspberry Piを持っている人は遊んでみて欲しい。
僕が無意識にカオスに惹かれる遠因のひとつは、やっぱり生物として文字通りカオスから生まれてきたからだろうな。面白いな。
2019-08-28 21:42
nice!(1)
コメント(0)



コメント 0