太さの変わるBezier曲線の生成 - その11

こないだから考えてるタブレットでPhotoshopのブラシの線を描いたようなBezier曲線を生成するソフトを作りたいという話についてコメントを頂いたうたひこさんから宿題をもらった。その宿題とは

1. ベジェ曲線同士の交点の取得方法
2. ベジェ曲線内のX、Y座標の最大値の取得方法
3. ベジェの（単純な）オフセットの方法

というもの。お、重い。

でもいずれ解決しなければいけない問題なのでここでこの宿題を先に考えたい。まず、ベジェ曲線同士の交点について。

ふたつのBezier曲線の交点

n次Bezier曲線の交点を求める問題はn次連立方程式を解く問題になるので3次のBezier曲線同士であっても一般的な解の公式として書き下せない。従って数値的に解くしかない。こういうとき困るのは

• 交点があるかどうか前もってわからない
• 交点がある場合は、ただひとつだけとは限らない

ということで、アルゴリズムとして

• 交点があるかどうかをまず調べる
• 交点がありそうならまずひとつ目を探す
• 他にありそうか調べる

というやりかたが一番まっとうな方法になる。ところがまたこれが面倒で交点があるかどうか簡単に知る方法が無い、ということが多い。

3次のBezier曲線の場合、M字型になることはないけどS字にはなり得るのでふたつの3次Bezier曲線の交点は最大9個ありえる。例えば制御点が

を持つふたつのBezier曲線は図-16のようになる。

このような曲線の交点をもれなく数値的に求めるというのはなかなか難しい。

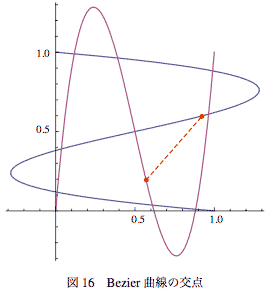
一般的な数値解法による交点の求め方

ここで突然ではありますが曲線上の点同士の距離を考える。

点列p₁を制御点とするBezier曲線をP₁(t)、同様にP₂(t)とする。それぞれのあるパラメータの値t₁、t₂に対する点の距離ρ(t₁,t₂)

を考えてみる。ここでP^x₁(t)などはP₁(t)のx成分であるとする（ノーテーションがくるくる変わるな。いかん）。

図-16の中に描いた赤い点の間の点線の長さが距離ρ(t₁,t₂)である。この距離ρ(t₁,t₂)が0となるパラメータの組(t₁,t₂)のところが交点となる。 この距離をふたつのパラメータに対してプロットしてみると、図-17のようになる。

大きな値（図が上の方）に対応する位置同士の距離は離れていて近いと下の方に来る。あたりまえだけど。 おなじ図を等高線表示で描いてみたのが図-18である。

これを見るとまんなかに大きな窪地があって、四隅にふたつずつ低いところがあることがわかる。このへこみは9個の交点に対応している。ためしにt₁=0.5、t₂=0.5のときの距離ρ(0.5,0.5)を計算してみると0になることがわかる。つまりt₁=0.5、t₂=0.5はこのふたつのBezier曲線の交点である。

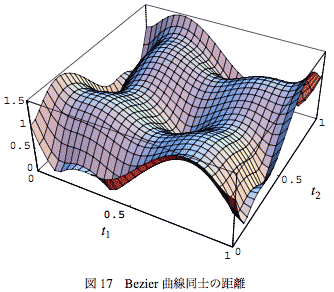
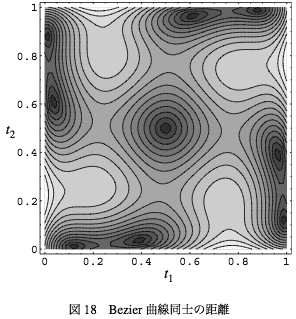
この2本は同じものを90°回転させたものなので距離のマップも対称性がよくわかりやすいが、一般のBezier曲線では複雑な地形になる。

3次のBezier曲線の交点を求める問題は最初に述べた2元連立3次方程式の根を求める問題として解いてもいいけど、それは数値計算するには面倒なことが多いので、この距離ρ(t₁,t₂)のような非負のスカラ関数の最小化問題と捉えた方が簡単で数値的にも安定な場合が多い。

また、3次Bezier曲線はパラメータtに関して3次（あたりまえ）なので力ずくで微分すればρ(t₁,t₂)のグラディエント

が計算できる。この値があれば収束計算が安定に速くできる。

収束計算のアルゴリズムにはいくつかあるけど、今回のような問題は比較的素性のいい問題と見なすことができるのでどれでもそれほど性能に差はない。また、交点が無い場合でも単に最小値でも大きな値にしかならなかったという結果になるだけでアルゴリズムが無限ループになったりすることが無いようにできる。これは非常に心強い。

具体的なアルゴリズムは例えばgslの「35 Multidimensional Minimization」のマニュアル（ここにバージョンは遅れてるけど日本語訳がある。ありがたや）に紹介がある。

Bezier Clipping法

以上はごく一般的な数値計算法による交点の求め方だけど、Bezier曲線の特徴を使った方法が考えられている。

たとえば、Bezier Clipping法という、東大の西田友是教授が発表された方法がある。

平面上の点列が与えられたとき、すべての点を含む最小の凸多角形を凸包と呼ぶ。Bezier曲線は制御点の凸包からはみ出ない、という性質があってこれを凸閉包性という。

図-19の左は3次の、右は5次のBezier曲線が青い線で描いてある。赤丸がそれぞれの制御点で、内部が草色の多角形が制御点の凸包である。

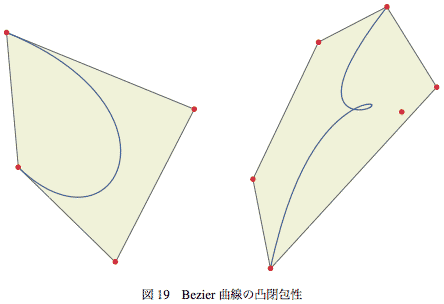
もし、ふたつのBezier曲線が交差するなら、その交点はそれぞれの凸包の共通部分に含まれる。図-20に赤青二本の3次Bezier曲線とそれぞれの制御点、および凸包を示す。

ふたつの凸包の重なった領域の内部に交点があることがわかる。 このあと、曲線の凸包の内部にある部分だけを切り出してきて、またその凸包を考え、その共通部分を取り出す。これを繰り返せば凸包の共通部分は交点の位置に収束する。

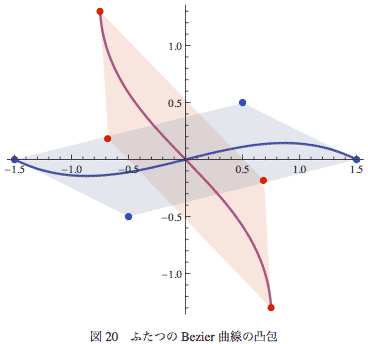
Bezier曲線は以前やったように簡単に分割できるのと、最初にやった単純な数値的解法とちがって、凸包は必ず入れ子になる（切り出したBezier曲線の凸包はもとの曲線の凸包に含まれる）ので繰り返しの過程で交点を逃してしまう心配が無く、安定な収束が期待できる。特に交点がひとつだけ（0でもなければふたつ以上でもない）ということが保証されている場合には強力な方法である。

しかし、例えば最初に上げた図-16のようにふたつの凸包がほとんど重なってしまうような場合は収束は遅くなるし、実装によっては収束しないこともありえる。

交点を持つか、持たないかの判定

そもそも交点があるかどうかわからない場合から始める必要がある方が一般的で、上の議論は 「交点がある場合にそれを求めるにはどうするか」ということで、まず、交点があるかどうかの判定をしなければいけない。

そのためには、まずざっくりと、ひょっとしたらあるか、それとも絶対ないか、ということを判定する必要がある。このためにさっきの制御点の凸包が使える。凸包に共通部分がなければ交点は持たないと言える。

ただ、この制御点による凸包は曲線にくらべてずいぶん大きいことが多い。もう少しタイトな凸包が欲しい。

また、複数の曲線がお互いに交点を持つかどうかを判断する場合、曲線の数が多くなると判断する回数は爆発的に増える。そこでこの判断はなるべく簡単にしたいが、一般の凸多角形の共通部分の計算は面倒なことが多い。

このとき、AABB（Axis Aligned Bounding Box）という、座標軸に平行な辺を持つ長方形を使えば、判断は簡単になる。2次元ゲームなどでAABBは当たり判定用に多く使われている。

次回、宿題のふたつ目としてこの、Bezier曲線のAABBを考える。おっと、その前にBezier曲線と直線の交点を求める話を先にやらなくては。でもワインを飲んで眠いのでもう寝る。