太さの変わるBezier曲線の生成 - その16

仕事が忙しくてなかなか進めることができない。しばらく触らないでいると何やってたかすぐ忘れてしまう。中途半端だけど、ちょっとでも書き進めることにする。こないだたどり着いたオフセット問題はBezier曲線で一般の曲線を近似するという問題に帰着することがわかった。その続き。

Bezier曲線による一般の曲線の近似

さて、この問題はかなり重い。解析的な方法で直接解を求めるようなやりかたは存在しないので、数値的な繰り返し収束計算が必要になる。

目標の数学まわりをまず整理しておく。

1. 近似対象の曲線は媒介変数表示されているとする
2. 連続で少なくとも1階微分可能な曲線であるとする
3. これを3次Bezier曲線で近似する
4. 近似精度のなんらかの基準を設ける
5. 近似精度以内にならない場合、Bezier曲線を分割して近似を進める
6. そのとき分割位置決定の方針も与える

とする。微分不可能な点を含む場合はそこでわけて別々のBezier曲線で近似すると考える。この4.と6.がキモになる。最終的には効率も問題になるけど、とりあえずそれはおいといて、筋道が数学的にわかりやすいところから攻略することにする。

曲線の近似精度（どれだけ近いか）を議論するためにはふたつの曲線の定量的な近さをなんらかの方法で定義してやる必要がある。まずそれから。

曲線同士の近さ

普通の陽に表された関数y=f(x)とy=g(x)同士の距離は例えば図-36のように

などで簡単に距離付けすることができる。この場合δは、曲線に囲まれた図中のハッチの部分の面積になってδが0のとき、そして0のときに限って二つの関数は一致している、ということになる。絶対値のかわりに2乗にしたり、定義域の長さで割ったりすることもあるが、考え方はどれも同じになる。

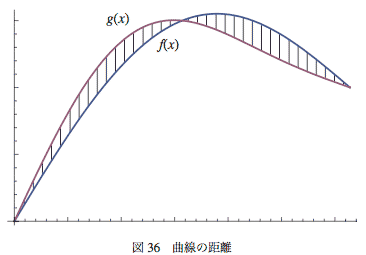
これをBezier曲線のような媒介変数表示された曲線に使おうとすると面倒が起こる。

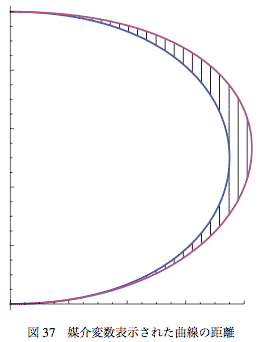
図-37のようなハッチのある部分の面積は式-36のような単純な積分では表されず、めんどうな場合分けが必要になる。また、媒介変数のds/dtが二つの曲線で一致しているとは限らず、変数tの同じ値にたいして必ずしも近い点となるとは限らない。従って積分変数を線分の長さsにとるなどの工夫が必要になる。

計算量は多くなっても、場合分けなどの面倒がない方が実装には向いている。

近さのめやす

ここで近似対象となる曲線をQ(r)、近似させたい3次Bezier曲線をP(t)とする。媒介変数は紛らわしいのでrとtに書き分けてある。 Q(r)のrに関する微分をQ'(r)

とする。Q(r)が2次元のベクトルなのでQ'(r)もふたつの要素を持つ。

Q(r)のあるr₀で曲線に垂直な直線は

と書ける。ここで下付き添字のx、yはx成分とy成分を表す。

図-38のようにこの直線とP(t)との交点を考える。これは以前にやったが、Bezier曲線と直線の交点を3次方程式の解として求まる。交点の位置でのtの値をt₀とする。

ここでδ

はQ(r)とP(t)が十分近ければ点Q(r₀)と曲線P(t)との距離と見なすことができる。ただし

であるとする。

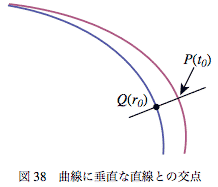
このδをrの定義域にわたって積分した

を曲線同士の距離とすることができる。つまり、Δが0のときに、そして0のときに限ってふたつの曲線は一致する。

この定義は非常に煩わしくて面倒に見える。が、図-37のような場合でも場合分けをする必要がない。ただし、このΔの値はハッチの面積には一致しない。

どっちみち繰り返しによる収束計算によって近似曲線を得るしかないので多少計算量が多くても安定な方が望ましい。

このやりかたを、具体的にBezier曲線で一般の曲線を近似する方法に適用してみる。でもそれはまた次回にしよ。