Zernike多項式 - その3 Zernike多項式の導出

Zernike多項式は単位円の中で直交する関数列である。そのような関数列はGram-Schmidtの直交化法などでいくらでも作ることができる。でも、その中で簡単で便利で役に立つ関数列はそれなりに工夫しないと作れない。

無限にある直交関数列のなかで、Zernike多項式はどういう特徴を持ったものなのか、その特徴を持つ具体的な関数の形を得るにはどうするか、という話。

Zernike多項式の具体的な表式を求める

多項式と言いながら極座標で書いてあるけど、これは実はデカルト座標（普通の直交座標）に変換すると、ρと最大次数は同じのxとyに関する多項式になる。

Zernike多項式の導き方をBorn&Wolfの第2巻の付録に従って大筋を追ってみる。

Zernike多項式生成の条件

単位円内で直交する関数系は無限にある。ある関数系に

1. 直交座標x、yに関する多項式である
2. 単位円内で直交する
3. 座標軸を回転させても形式は変わらない

と言う条件を課すことにする。最後の条件は直交座標の原点の周りの回転

を行ったとき多項式系V_i(x,y)が

と変換できる、と言う意味である。ここでG_i(θ)は2πを周期に持つ連続な周期関数である。この最後の条件がキモでZernikeさんのえらいとこ。

この条件を満足する多項式V_i(x,y)は、まず三つ目の条件から、mを整数として

の形でなければならない（というかこれしかない。これしかない、というこをどうやって証明したらいいのかわからないけど、これしか思いつかない）。従って一般にV_i(x,y)は複素関数となる。

式-9から直交条件は（複素関数であることを考慮して）

となってふたつの積分に別れる。ここでA^†はAの複素共役を表す。また、積分範囲のCは単位円の内部であるとする。

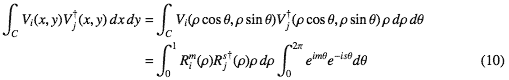
後ろのθに関する積分はm=sのとき以外は0になるのでV_i(x,y)が直交するためには同じmに対してR_i^m(ρ)が単独で直交している必要がある。

さらに、V(x,y)がx、yのn次の多項式だとすると

1. R_i^m(ρ)はρのたかだかn次の多項式
2. -n ≦ m ≦ n
3. n-|m|は偶数
4. R_i^m(ρ)はρ^|m|以下の次数を含まない

となっているはずである。3番目の性質は

でなければならないのでR_i^m(ρ)はmが偶数のとき偶関数、奇数のとき奇関数となるからである。

また最後の性質は多項式の最低次数がμだった場合、(ρ*cosθ)^μや(ρ*sinθ)^μからe^iμθのような係数が現れるが、e^imθをくくり出すためには少なくともμ≧mでなければならないからである（μ=m+ν（ν≧0）ならe^imθe^iνθとできる）。

動径関数の具体的な生成

ということで動径関数R_i^m(ρ)は、上の制限を満足するnとmの添字ふたつの組み合わせで指定できるはずである。従って抽象的な添字iの代わりに具体的な次数nと回転数mのふたつを使えばいいということになる。

ということであとは、あるmの値に対してρのベキの列（ρ^|m|、ρ^|m|+2、ρ^|m|+4...）からGram-Schmidtの直交化法でもなんでも使って順番に直交列を作れば動径関数R_i^m(ρ)が得られる。

でもそういうやりかただと無限個あるmそれぞれについて無限回直交化をやらないといけないので、うまく一般項の形が表現できればいいけど思いつかなければ厳しい。Born&Wolfでは動径関数列をJacobiの超幾何多項式から作っている。見慣れないので難しいけど、Jacobiの超幾何多項式の性質から直接動径関数の一般形が得られる。

Born&Wolfから結果を引き写すと

だそうである。うーん。よくわからんけどすごい。これだと具体的にnとmの値を与えれば多項式の形が計算できる。Gram-Schmidtをやっていってこれを導くのはひらめきがないと無理だろうな。

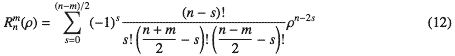
ちなみに、Born&Wolfのこの部分の導出は「さて、周知のようにJacobiの（超幾何）多項式は、云々」となっていて突然Jacobiの超幾何多項式が現れる。Jacobiの超幾何多項式が「世間一般に広く知れ渡っている」かなあ？まるで八百屋のオヤジに訊いたら「らっしゃい！　Jacobiの超幾何多項式？　あるよっ、もう(0,1)で直交化できてるからあとは軽く茹でておひたしとかでもいいよっ、味噌汁にも合うしねっ！」と言う感じ。

式-4のR_i^m(ρ,θ)は、式-9のVに添字をつけて

とすればよい（実関数が作れる）ということになる。

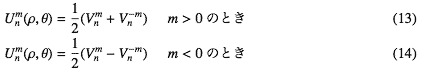
Zernikeさんは正規化

のかわりに

とした。この方がρのベキの係数がうまく整数になって式がシンプルになる。さすがノーベル賞。

詳細はBorn&Wolfの第2巻を参照していただきたい。

ちょとハードな数学が続いたけど、今回の内容に基づいて次回はこの多項式列の並べかたについて。