曲がった迷路その27 - バイキュービック補間の間違い [曲がった壁を持つ迷路の生成]
間をおくとすぐわからなくなってしまうので、昨夜はほぼ徹夜でごりごりと一段落するまで書いていた。そこで気がついた。
以前バイキュービック補間の係数を導いた。これが間違っていることがわかった。
バイキュービック補間をするクラスを書いて動作のデバグをしていたら、補間結果がでこぼこしている。なめらかな関数を補間しても最大10%以上のでこぼこができてしまう。
あれえ、おかしいなあと思いながら1次元にして詳しく見てみると、格子点の上で補間した曲線が折れ曲がっている。これはあきらかに微分可能になっていない。なんじゃ、こりゃ。
 とした。これはx=0で微係数は0だと思い込んでいて、それを前提に話を進めていたけど、ちゃんと微分してx=0での値を求めると
とした。これはx=0で微係数は0だと思い込んでいて、それを前提に話を進めていたけど、ちゃんと微分してx=0での値を求めると
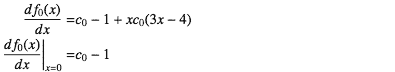 となって0にならない。これはあたりまえで、そもそも3次のベキ関数で、区間[0,1)で両端の値とそこでの微係数を決めると係数はすべて決まって、c0のような遊んでる係数が残るはずがない。大ボケだった。
となって0にならない。これはあたりまえで、そもそも3次のベキ関数で、区間[0,1)で両端の値とそこでの微係数を決めると係数はすべて決まって、c0のような遊んでる係数が残るはずがない。大ボケだった。
ということでお詫びの上、以下に修正する。
N×Mの格子点上のデータAi,jの2次元のシンク補間というのは、ある点(x,y)での値A(x,y)が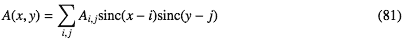 とするもので、
とするもので、
 である。
である。
その近似的な補間というのは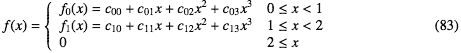 とするという意味である。これを区間ごとにシンク関数に近似する。ただし、[2,∞)ではずっと0で、シンク関数とは似ても似つかないものなので区間[1,2)ではちょっと味付けをする必要がある。
とするという意味である。これを区間ごとにシンク関数に近似する。ただし、[2,∞)ではずっと0で、シンク関数とは似ても似つかないものなので区間[1,2)ではちょっと味付けをする必要がある。
 とする。
こうするとc00は1でc01は0なのがあきらかで、
係数を連立方程式として解くまでもなく
とする。
こうするとc00は1でc01は0なのがあきらかで、
係数を連立方程式として解くまでもなく
 となる。以前やった最小2乗法的に決める係数は残らない。
となる。以前やった最小2乗法的に決める係数は残らない。
 とするということである。
ここで最後の式は、もとのシンク関数の微係数の値が1/2なので、近似になっていない。これはその外の区間[2,∞)がずっと0で、従ってx=2で微係数がジャンプしてしまうのを避けるためである。
とするということである。
ここで最後の式は、もとのシンク関数の微係数の値が1/2なので、近似になっていない。これはその外の区間[2,∞)がずっと0で、従ってx=2で微係数がジャンプしてしまうのを避けるためである。
これも連立方程式として解くまでもなく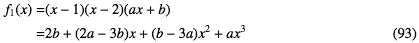 の形でなければならないので、上式を微分すればすぐ
の形でなければならないので、上式を微分すればすぐ
 であることがわかる。
であることがわかる。
これで普通に使われているバイキュービック補間の補間関数と一致した。
以前は係数がすべて整数になっているのは、効率上の問題だろうなどと言ってたけど、それは真っ赤な嘘で、条件を上のように決めればシンク関数の値がたまたま簡単な値なので、そうなるというだけの話である。計算効率は無関係。
ということで訂正します。
一段落したので今から寝よ。
以前バイキュービック補間の係数を導いた。これが間違っていることがわかった。
バイキュービック補間をするクラスを書いて動作のデバグをしていたら、補間結果がでこぼこしている。なめらかな関数を補間しても最大10%以上のでこぼこができてしまう。
あれえ、おかしいなあと思いながら1次元にして詳しく見てみると、格子点の上で補間した曲線が折れ曲がっている。これはあきらかに微分可能になっていない。なんじゃ、こりゃ。
バイキュービック補間の間違い
実装ではなく、もとの式が間違っていることがわかった。もともとx=0で微分可能でない式になっていた。 式-32をもう一度書くと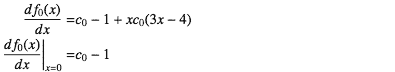
ということでお詫びの上、以下に修正する。
バイキュービック補間係数を求める
バイキュービック補間の考え方は- 画像のような2次元格子点上のデータを、もともと稠密だったもののサンプリングである、とみなす
- サンプリングはサンプリング定理を満たした上で行われているとする
- とするとシンク関数で補間できる
- シンク補間はある点の補間の値を知るためにはすべての格子点の値が必要となる
- それは計算量が多いのと、シンク補間は遠くの点からの寄与は小さくなるので、近傍の点からだけで近似的なシンク補間を行う
N×Mの格子点上のデータAi,jの2次元のシンク補間というのは、ある点(x,y)での値A(x,y)が
その近似的な補間というのは
- ある点(x,y)での補間値を(x±2,y±2)に含まれる格子点だけを使う
- シンク関数の近似関数は区間ごとの3次ベキ関数を使う
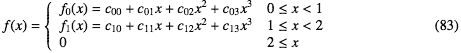
[0,1)区間
ここでは格子点x=0とx=1の位置でシンク関数の値とその微係数が一致するとする。 つまり
[1,2)区間
こっちの区間は以前やったのと同じになる。もう一度繰り返すと
これも連立方程式として解くまでもなく
これで普通に使われているバイキュービック補間の補間関数と一致した。
以前は係数がすべて整数になっているのは、効率上の問題だろうなどと言ってたけど、それは真っ赤な嘘で、条件を上のように決めればシンク関数の値がたまたま簡単な値なので、そうなるというだけの話である。計算効率は無関係。
ということで訂正します。
一段落したので今から寝よ。
2009-08-01 07:21
nice!(0)
コメント(0)
トラックバック(0)


コメント 0