近軸光線追跡 - その3

こないだから近軸マトリクスをMathematicaで実装するにあたって近軸理論をおさらいしている。球面の境界での屈折で、無収差の条件がふたつある、というちょっとした寄り道話。

3.3  式-13が式-17と一致する条件

O₂の位置がPによらなくなるような条件がある。

そのひとつはp₁=p₂=0である。このときは式に代入するまでもなく式-13と式-14が同時に成立する。これはつまり球面の中心から光が出る場合で、境界面では常に垂直入射となっている。平面での屈折の場合の無限遠と同じ条件であるとみなせる。

それとわかりにくいが実はもうひとつある。

としてみる。この場合、

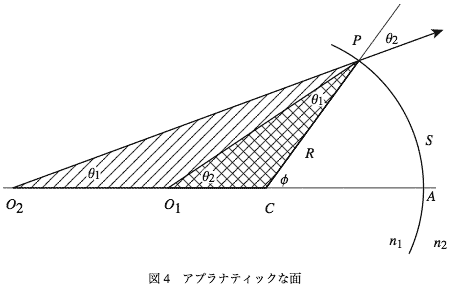図-4のように三角形CPO₁とCO₂Pは角O₁CPが共通なので相似な三角形になる。この場合Pの位置が円周上ならどこにあろうと相似になる。つまり

となる。この場合、式-13と式-14は同じ式になって（式の変形がわずらわしいのでここには書かない）、すなわち点Pの位置（υ₁の値）が変わってもυ₂がそれに従って変わるだけでp₂に影響しない、つまりこの場合に限りO₂の位置はυ₁によらず動かない、ということになる。ただし、当然p₁とp₂は同符号、つまり面に対して同じ側になければならない。

これをアプラナティックな面（Aplanatic Surfaces）、式-18あるいは同値な条件をアプラナティック条件などと呼ぶことがある。収差を発生させずに面の屈折力を利用でき、高N.A.の顕微鏡対物などによく使われる。アプラナティックの条件は球面の場合にだけ現れる特殊な例であるが、非常に面白い（こんな条件、言われなければ絶対気がつかない）し、レンズ設計上は重要である。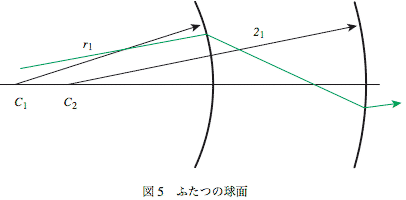

3.4  ふたつ以上の境界面がある場合

図-のようにもうひとつ球面の境界面がある場合を考える。光線はひとつめの境界で屈折し、その屈折光線がもうひとつの面に到達してさらに屈折する場合を考える。

ふたつの球面の中心を結ぶ直線は回転対称軸となる。この対称軸を光軸と呼ぶ。球面の境界面が1枚の場合には光線の出発点と境界面の中心を結んだ線を光軸とした。これは系の対称性からきた概念である。ふたつの面がある場合、近軸領域は光線の出発点も制限を受けることになる。

さらに言えば、厳密には境界面3枚以上の場合には光軸は存在しない。その場合、3枚目以降の面は最初の光軸の上に並んでいるとするか、近似的にそうみなすことができないと光軸は仮定できない。

ということで面が複数枚ある場合には、近軸領域とは、光軸に近い点から出発して、ほぼ光軸にそって進む光線だけを考えることになる。

光軸に近いある点Qを通ってQと光軸を含む平面内を進む光線を考える。 ここで光線が光軸からの距離をhとして

R_nはそれぞれの境界面の半径である。

このとき一つの面について近軸領域とみなすことができれば他の面にとっても近軸領域とみなせる。