楽譜アーカイブアプリ - その21 Bicubicの場合 [考え中の問題]
一昨日、画像補間に関してちょっと思うことができたので、寄り道をはじめた。まえやったBicubic補間がなにをやっているか、のおさらい。
sinc関数そのものはx=0から遠くなると小さくなる、つまり遠い点からの影響は小さくなるので、誤差が無視できる適当なところで打ち切るようにしたくなるのが人情である。そこでBicubicでは周辺±2個の格子点までを考慮してその外は無視する。つまり図-8.1の|x| > 2では恒等的に0である、とするのである。
しかしそのままではx = ±2の点で微分不可能になる。これでは補間した結果にグリッジ(Glitch折れ曲がり)がでるので始末が悪い。そこで±2のところでは微係数が0になるように、つまり滑らかに恒等的に0の領域につながるようにしたのがBicubic法である。具体的に言えば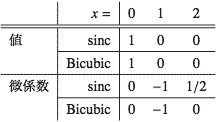 として、さらにどうせ違う関数になるので、Splineフィットの考え方を使って区間ごとの3次のベキ関数で近似してしまおうというのがBicubic法の関数である。これは補間すべき点のまわりの格子点のうち距離が2以下の4点から値を計算する。従って2次元の場合は都合16点である。詳細は以前まとめたのでそれを参照してほしい。
として、さらにどうせ違う関数になるので、Splineフィットの考え方を使って区間ごとの3次のベキ関数で近似してしまおうというのがBicubic法の関数である。これは補間すべき点のまわりの格子点のうち距離が2以下の4点から値を計算する。従って2次元の場合は都合16点である。詳細は以前まとめたのでそれを参照してほしい。
8.1.3 sinc補間の問題に対するBicubic法の解決策
ところが、式-8.3からわかるように、このsinc関数による補間ではひとつの補間点の値を知るためにはすべての格子点の値が必要になる。これは計算量的に重い。例えばもし格子点の間に中点をとってそこの値を補間するような、格子点の数を単純に倍にする、というようなことをしたいなら、式-8.3をバカ正直に計算するよりFFTと逆FFTをした方が、結果はまったく同じで計算量は激減する。実際にそういう方法で補間する場合もある。sinc関数そのものはx=0から遠くなると小さくなる、つまり遠い点からの影響は小さくなるので、誤差が無視できる適当なところで打ち切るようにしたくなるのが人情である。そこでBicubicでは周辺±2個の格子点までを考慮してその外は無視する。つまり図-8.1の|x| > 2では恒等的に0である、とするのである。
しかしそのままではx = ±2の点で微分不可能になる。これでは補間した結果にグリッジ(Glitch折れ曲がり)がでるので始末が悪い。そこで±2のところでは微係数が0になるように、つまり滑らかに恒等的に0の領域につながるようにしたのがBicubic法である。具体的に言えば
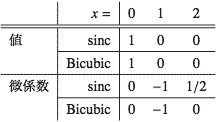
2011-01-11 22:25
nice!(0)
コメント(0)
トラックバック(0)


コメント 0