楽譜アーカイブアプリ - その22 Lanczosの場合

昨日は以前やったBicubic補間の思想をおさらいした。考え方は理解しやすい。今日は本題のLanczos補間の考え方について。

8.1.4  sinc補間のもうひとつの問題に対するLanczos法の解決策

さらにもうひとつ問題がある。図-8.1を見ればわかるように正と負を行ったり来たりする。これは隣り合う格子点の値が大きく異なるような（一方は大きくて一方は小さいというような）ところでは値の大きな点の影響で小さな点の近くにこの振動が現れたりする。また、光の強度などのような負の値をとらない量であっても、補間の結果がこの振動のせいで負になる場合もある。これは困った問題である。

そこで、周辺の「ひらひら」がsinc関数よりも小さいものがありがたい。で、Lanczosさんは簡単な関数を思いついた。前も書いたが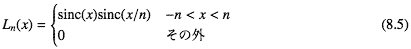

というようなものである。ここでnは整数で、±nの格子点までを考慮して、その外では無視する。従ってn=2の場合はBicubicと格子点の使い方は同じになる。

この関数は本来のsinc関数（ひとつめのsinc関数）をふたつめの広がりの大きなsinc関数で押さえ込むようになっていて、ちょうどx = ±nのところではBicubicと同じように微係数も0になっている。n=2 〜 5のL_n(x)をプロットしたのが図-8.2である。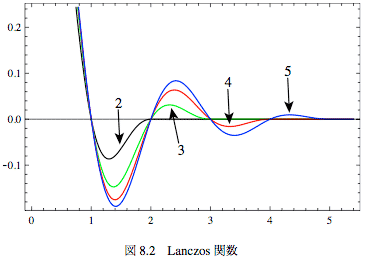

あたりまえだけど、nが小さい方が「ひらひら」も小さいことがわかる。図-8.3に、もとのsinc関数からの差を示す。

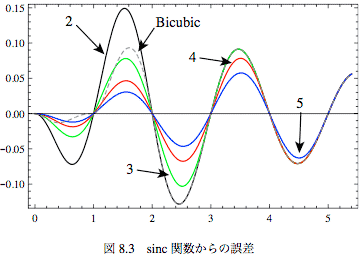図中比較のためBicubicの差も点線で入れてある。ぱっとみて、けっこうちがってんじゃん、と言う印象である。ところがこのLanczos補間を画像の補間に使うと、見た目はいいらしい。

sinc関数で定義通りに補間するとサンプリングによるカットオフ周波数より低い成分は変化させず、高い成分はすべて0になる。すなわち周波数プロファイルはまったく変化しない。ところがBicubicを含めてこれらの補間はもとのサンプリングよる周波数帯域よりも高い成分を作り出す。特にLanczos補間はFourier領域でどういう効果を持つか考えてみれば理解できるはず。その意味でもともと存在していなかった情報を付加している、ということになる。sinc関数よりも見た目が良くなるというのは、頑固な真実よりも口当たりのいい嘘のほうがいい、ということなのか。

コメント 1

沒有醫生的處方
buy cialis http://cialisvonline.com/ 200 cialis coupon
by Cialis 20 mg best price (2018-04-15 06:30)