厳密な光線追跡 - その6 [光線追跡エンジンを作る]
前回、球面と光線との交点を求める式を導いた。面白い形に整理できて、この形を他所で見たことがないんだけど、これってあたりまえなの?あんまり当たり前のことを書いてもしかたない。
まあとりあえずいいとして、今日は球面の延長としての2次曲面の交点を求める問題を整理して、そのあと非球面の場合をちょこっと考察する。非球面はいろいろ問題が多いので次回にまたがることになる。
光学では2次曲面もさっきの球面に似た式が使われることが多い。つまり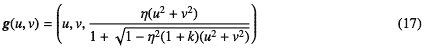 のような式である。球面の式-15と較べるとkという定数が入っているだけの違いである。
のような式である。球面の式-15と較べるとkという定数が入っているだけの違いである。
このkをconic constantと呼ぶ。この値によって
などになることは式-17を良く知っている陰関数の形に変形すればわかる(面倒なのでここではやらない)。この式は球面も含めて2次曲面が統一的に表現できるのと、kの値に関わらず原点を通るので便利である。
ただし、流儀によってはkのかわりに−kを使ったり、1+kをkとしたりと言う場合があるので注意が必要である。もちろん流儀それぞれに理由があってメリットでメリットがある(微妙な差ではあるけど、式の形を覚えていようと思うと不便)。
球面の場合と同じように光線との交点を求めるためのαを解くと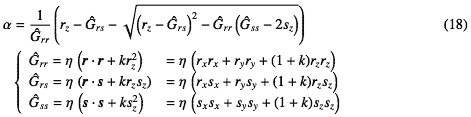 となる。式-18は球面の場合の式-15と同じ形をしているが、単なる内積だった定数がちょっとz方向に変形している。微妙な違いだけど、こういうふうに整理できること自体はなんだか面白い。
となる。式-18は球面の場合の式-15と同じ形をしているが、単なる内積だった定数がちょっとz方向に変形している。微妙な違いだけど、こういうふうに整理できること自体はなんだか面白い。
交点を求める問題としては、このあと球面と同じことをすればいい。
非球面はこれまでと同じ媒介変数表示すると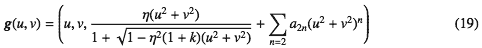 である。つまり2次曲面にベキの項がくっついた形をしている。普通の書き方をすれば
である。つまり2次曲面にベキの項がくっついた形をしている。普通の書き方をすれば
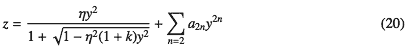 で、この書き方はCodeVやZemaxで使われている表現である。
で、この書き方はCodeVやZemaxで使われている表現である。
ベキは普通はn=5つまり10次まで使われるが、それ以上使うこともあるし、2次の項や、奇数次の項が使われることもある。
個人的には2次の項を使うとηが光軸での面の曲率に一致しなくなるので使うべきではない(近軸が無意味になる)と思うし、奇数次の項は数学的に美しくない(微係数の扱いが一貫しない。絶対値? 連続な関数なのにわざわざ??? 高校数学やり直したほうがええでぇ)ので僕はキライである。こういうのを使う人の設計はただの結果オーライが多いような気がするが、まあそれはどうでもいい。
奇数次や2次の項を使いたくなる原因はベキ関数で表現できる形状がそれほど自由ではない、ということである。ベキ関数にも限界はあって、その上数値計算に利用しようとするとさらに別の限界に阻まれる。非球面式は光学の問題に対して一般的な形に見えるので、みんな思考停止的に非球面式を使ってるけど、本来は問題それぞれに固有の表現があってしかるべきである、と僕は思う。少なくとも非球面は万能ではない。
まあそれはいいとして、非球面の場合はまず2次曲面(非球面式のベキのない部分)と光線との交点を求め、それを初期値にして収束計算をするのが手っ取り早い。ベキの項があまり大きくなければ収束ははやい。
そこに問題がある、と言う話は次回。
まあとりあえずいいとして、今日は球面の延長としての2次曲面の交点を求める問題を整理して、そのあと非球面の場合をちょこっと考察する。非球面はいろいろ問題が多いので次回にまたがることになる。
3.3.3 2次曲面の場合
2次曲面が屈折面として使われることはあまりないけど、解析的に解が求まる面のひとつなので示しておく。また、非球面の場合の収束演算の初期値として使えるのでプログラミング上は有用である。光学では2次曲面もさっきの球面に似た式が使われることが多い。つまり
このkをconic constantと呼ぶ。この値によって
| k < −1 | : | 双曲面 |
| k=−1 | : | 放物面 |
| −1 < k < 0 | : | 楕円面(ラグビーボール形) |
| k=0 | : | 球面 |
| 0 < k | : | 楕円面(アンパン形) |
ただし、流儀によってはkのかわりに−kを使ったり、1+kをkとしたりと言う場合があるので注意が必要である。もちろん流儀それぞれに理由があってメリットでメリットがある(微妙な差ではあるけど、式の形を覚えていようと思うと不便)。
球面の場合と同じように光線との交点を求めるためのαを解くと
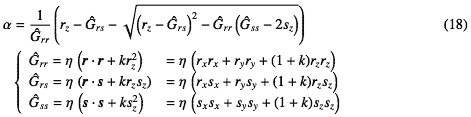
交点を求める問題としては、このあと球面と同じことをすればいい。
3.3.4 非球面および一般の面
非球面と光線の交点を求めるには非線形な高次方程式を解かないといけない。これは球面の場合のように解を解析的に表現しておいてあとで数値計算する、というわけにはいかない。従って収束計算を用いることになる。非球面はこれまでと同じ媒介変数表示すると
ベキは普通はn=5つまり10次まで使われるが、それ以上使うこともあるし、2次の項や、奇数次の項が使われることもある。
個人的には2次の項を使うとηが光軸での面の曲率に一致しなくなるので使うべきではない(近軸が無意味になる)と思うし、奇数次の項は数学的に美しくない(微係数の扱いが一貫しない。絶対値? 連続な関数なのにわざわざ??? 高校数学やり直したほうがええでぇ)ので僕はキライである。こういうのを使う人の設計はただの結果オーライが多いような気がするが、まあそれはどうでもいい。
奇数次や2次の項を使いたくなる原因はベキ関数で表現できる形状がそれほど自由ではない、ということである。ベキ関数にも限界はあって、その上数値計算に利用しようとするとさらに別の限界に阻まれる。非球面式は光学の問題に対して一般的な形に見えるので、みんな思考停止的に非球面式を使ってるけど、本来は問題それぞれに固有の表現があってしかるべきである、と僕は思う。少なくとも非球面は万能ではない。
まあそれはいいとして、非球面の場合はまず2次曲面(非球面式のベキのない部分)と光線との交点を求め、それを初期値にして収束計算をするのが手っ取り早い。ベキの項があまり大きくなければ収束ははやい。
そこに問題がある、と言う話は次回。
2012-10-01 21:36
nice!(0)
コメント(0)
トラックバック(0)


コメント 0