最小2乗法 - その1 [最小2乗法のイメージ]
最近ときどきやっている知り合いのお手伝い。その中でカメラで撮った強度分布を最終的にある関数でフィットする必要が出てきて、こないだから前処理をちまちまとコーディングしている。カメラの1フィールド以内に計算を終わらせる必要があるが、この問題自身はそれほど難しくないし、ここで詳細を開陳してもあまり面白いことはない。
しかし、最近数値計算プログラムを書くことがめっきり少なくなっていて、あれだけ昔いろいろな場面でお世話になった最小2乗法もすっかり忘れてしまった。
ボケ防止の意味も含めて思い出そう。ちょっとコーディングにも飽きたし。最終的にはHouseholder変換を使って最小2乗法で係数を求めるObjective-Cのクラスを実装しよう....
会社に入ってすぐくらいのころ、ある測定機のデータを整理するために最小2乗法のルーチンが必要になった。データが格子点にあるのでまずモデル関数列をGram-Schmidtで離散的に直交化して、その解からもとのモデル関数の係数を計算するような書き方だった(参考にした論文がそうしていた)。そのあと、Householder変換を勉強してそれでQR分解するようなやりかたに書き換えた。最初はpascal(!)で、そのあとそれをCに書き換ていつまでも使い続けていた。
そのころはLAPACKやgslはまだなかったし、LAPACKの前身のLINPACKは名前しか知らなかった。実装先のHPのワークステーションには数値計算ライブラリがあったが別売で、高嶺の花だった。ようするにいまだにそう言う30年前の時代のやりかたをしているということだ。
でも、いいんだよ。僕は車輪の再発明が好きなんだ。
今回もあまり数学的な厳密さは追わずにイメージを得ることを優先して、証明などはやらない。証明は数学的にちゃんとしたひとがちゃんとやってくれていて、そちらを見てもらえばいい。僕はそう言うちゃんとしたひとではなくて一介の技術屋なので、現場の技術屋らしいことを書かないと存在意義がない。
以前イメージが大切だとえらそうに言ったのに、具体的な例を示さずにいたが、今回の最小2乗法はまとまりもいいのでイメージの例としてはちょうどいい。
ということで今回は珍しく、ある程度基礎的なところから始めて数学のイメージをまとめてから実装に入ろう。何のためかと言うと、最小2乗法を勉強しよう、というひとのために、それと僕自身のボケ防止のために。もちろんWebにはすでにいろいろな最小2乗法に関する解説がたくさんあるので、僕ならでは、という内容にしよう。
これまで基礎的なところはすっ飛ばすのが僕のやり方だったけど、たまには親切にやろう。
とは言っても、線形代数と数値解析の基礎的な知識は前提にする。ということで、始める。
最小2乗法の出番は、測定データ列から扱いやすいパラメータを抽出する、というような場面である。エクセル好きのひとがデータを直線近似して相関係数を出したりする、ああいうやつである。ほんとはもう少し難しいこともできて、ベキ関数列でフィッティングするなんてことにも使う。さらにおもてには現れないけど、ノイズの中から特定の周波数スペクトルを抜き出す、レンズの収差をZernike多項式で展開する、なんてときも実は同じことをしていると言っていい。
もう少し一般的に書くと、ある実数の入力列xi,(i=1,2...,n)に対して(このxiはスカラではなくベクトルでもあとの議論はそのまま使える)、やはり実数の測定値yiの組 があるとき、
があるとき、
 という関数f(x)を想定する。この関数はiには依存しないとする。またここでϵiは想定していないiに依存する因子、たとえば測定誤差や外乱などを一手に表しているとする。ϵiを直接知る方法はない(あればf(x)を確定することができるので、最小2乗法など必要ない)が、測定を通して平均値0の正規分布であるとする。ϵiの主な要因が例えば熱雑音のようなものであればこの仮定はそれほど間違ってはいない。このϵiに対する仮定は最小2乗法による結果の「もっともらしさ」に影響するんだけど、ここではあまり突っ込まないで、あとでちょっとだけ思い出すことにする。
という関数f(x)を想定する。この関数はiには依存しないとする。またここでϵiは想定していないiに依存する因子、たとえば測定誤差や外乱などを一手に表しているとする。ϵiを直接知る方法はない(あればf(x)を確定することができるので、最小2乗法など必要ない)が、測定を通して平均値0の正規分布であるとする。ϵiの主な要因が例えば熱雑音のようなものであればこの仮定はそれほど間違ってはいない。このϵiに対する仮定は最小2乗法による結果の「もっともらしさ」に影響するんだけど、ここではあまり突っ込まないで、あとでちょっとだけ思い出すことにする。
任意の関数f(x)とすると自由度が大きすぎて難しいので、関数列gk(x),(k=1,2,...m)の線形結合 と考えて、その係数ak,(k=1...m)を決定することを考える。つまりn個の測定値からm個のパラメータを決定する、という問題だと考える。
と考えて、その係数ak,(k=1...m)を決定することを考える。つまりn個の測定値からm個のパラメータを決定する、という問題だと考える。
例えば直線近似だと として、係数aとbを決定する問題だと考える。この関数列gk(x),(k=1...m)はもとの物理現象に自然なものを選んだり、あとの扱いが便利になるようなものを選んだりする。例えばなにかの振動を測定するような場合には三角関数を使うのが自然だし、単純な冪級数は汎用性が高くてしかもわかりやすい。
として、係数aとbを決定する問題だと考える。この関数列gk(x),(k=1...m)はもとの物理現象に自然なものを選んだり、あとの扱いが便利になるようなものを選んだりする。例えばなにかの振動を測定するような場合には三角関数を使うのが自然だし、単純な冪級数は汎用性が高くてしかもわかりやすい。
またこの関数列gk(x)は直交関数列のほうが実はぜんぜんいいんだけど、ここではそう仮定はしないでおく。
ちなみに直交関数列とは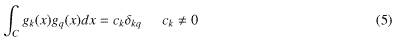 を満たすような関数列である。ここでCは関数列が定義された領域で、δkqはクロネッカーのデルタ、ckは関数列を指定する添字で決まる定数である。つまり、関数列の中の異なる添字の関数をふたつかけ算して積分するとすべて0になって、添字が同じ場合だけ0でない数字になるような関数列である。これが実は重要であることをあとで示したい。
を満たすような関数列である。ここでCは関数列が定義された領域で、δkqはクロネッカーのデルタ、ckは関数列を指定する添字で決まる定数である。つまり、関数列の中の異なる添字の関数をふたつかけ算して積分するとすべて0になって、添字が同じ場合だけ0でない数字になるような関数列である。これが実は重要であることをあとで示したい。
とりあえず今日はここまでにしてもう寝よう。
しかし、最近数値計算プログラムを書くことがめっきり少なくなっていて、あれだけ昔いろいろな場面でお世話になった最小2乗法もすっかり忘れてしまった。
ボケ防止の意味も含めて思い出そう。ちょっとコーディングにも飽きたし。最終的にはHouseholder変換を使って最小2乗法で係数を求めるObjective-Cのクラスを実装しよう....
1 はじめに
はっきり言って、べつに最小2乗法なんてLAPACKを使えばいいし、LAPACKのFORTRANインターフェイスがいやならgslもある。また好きな人も嫌いな人も多い「Numerical Recipe in C」にもちゃんと含まれている。いまさら自分で実装するまでもなくアルゴリズムは確立されていて、そういう既存の実績のあるルーチンを使った方が信頼性が高いし、速いし、手間も少ない。会社に入ってすぐくらいのころ、ある測定機のデータを整理するために最小2乗法のルーチンが必要になった。データが格子点にあるのでまずモデル関数列をGram-Schmidtで離散的に直交化して、その解からもとのモデル関数の係数を計算するような書き方だった(参考にした論文がそうしていた)。そのあと、Householder変換を勉強してそれでQR分解するようなやりかたに書き換えた。最初はpascal(!)で、そのあとそれをCに書き換ていつまでも使い続けていた。
そのころはLAPACKやgslはまだなかったし、LAPACKの前身のLINPACKは名前しか知らなかった。実装先のHPのワークステーションには数値計算ライブラリがあったが別売で、高嶺の花だった。ようするにいまだにそう言う30年前の時代のやりかたをしているということだ。
でも、いいんだよ。僕は車輪の再発明が好きなんだ。
今回もあまり数学的な厳密さは追わずにイメージを得ることを優先して、証明などはやらない。証明は数学的にちゃんとしたひとがちゃんとやってくれていて、そちらを見てもらえばいい。僕はそう言うちゃんとしたひとではなくて一介の技術屋なので、現場の技術屋らしいことを書かないと存在意義がない。
以前イメージが大切だとえらそうに言ったのに、具体的な例を示さずにいたが、今回の最小2乗法はまとまりもいいのでイメージの例としてはちょうどいい。
ということで今回は珍しく、ある程度基礎的なところから始めて数学のイメージをまとめてから実装に入ろう。何のためかと言うと、最小2乗法を勉強しよう、というひとのために、それと僕自身のボケ防止のために。もちろんWebにはすでにいろいろな最小2乗法に関する解説がたくさんあるので、僕ならでは、という内容にしよう。
これまで基礎的なところはすっ飛ばすのが僕のやり方だったけど、たまには親切にやろう。
とは言っても、線形代数と数値解析の基礎的な知識は前提にする。ということで、始める。
2 最小2乗法
「最小2乗法とは」というのはWikipediaでも読んで欲しい。僕よりちゃんと説明してくれる。たまには親切に、とか言っていながら全然親切じゃないな。まあいい、定義に僕らしさを出すなんてできないからな。最小2乗法の出番は、測定データ列から扱いやすいパラメータを抽出する、というような場面である。エクセル好きのひとがデータを直線近似して相関係数を出したりする、ああいうやつである。ほんとはもう少し難しいこともできて、ベキ関数列でフィッティングするなんてことにも使う。さらにおもてには現れないけど、ノイズの中から特定の周波数スペクトルを抜き出す、レンズの収差をZernike多項式で展開する、なんてときも実は同じことをしていると言っていい。
もう少し一般的に書くと、ある実数の入力列xi,(i=1,2...,n)に対して(このxiはスカラではなくベクトルでもあとの議論はそのまま使える)、やはり実数の測定値yiの組
任意の関数f(x)とすると自由度が大きすぎて難しいので、関数列gk(x),(k=1,2,...m)の線形結合
例えば直線近似だと
またこの関数列gk(x)は直交関数列のほうが実はぜんぜんいいんだけど、ここではそう仮定はしないでおく。
ちなみに直交関数列とは
とりあえず今日はここまでにしてもう寝よう。
2013-11-18 22:48
nice!(0)
コメント(0)
トラックバック(0)


コメント 0