最小2乗法 - その2 [最小2乗法のイメージ]
今日は、昨日の式-3、つまり
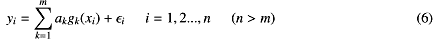 となるような係数akを測定値から決めればいいんだけど、ϵiがわからないのにそれをどうやってやるか、という話になる。とりあえず前準備みたいな話ではあるので、ちょっと退屈かもしれないけど、映画でもでだしの20分を飛ばすとあとがわからなくなるのは同じなのでもう少し付き合って欲しい。
となるような係数akを測定値から決めればいいんだけど、ϵiがわからないのにそれをどうやってやるか、という話になる。とりあえず前準備みたいな話ではあるので、ちょっと退屈かもしれないけど、映画でもでだしの20分を飛ばすとあとがわからなくなるのは同じなのでもう少し付き合って欲しい。
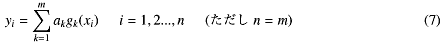 という、普通の(式と変数の数が一致した)連立1次方程式として解くことができる(もちろん関数列の選び方によっては解けない場合もある)。例えば2点のデータで式-6の係数を決めるというような場合で、これはその2点を結ぶ直線が得られる。しかし測定の際のϵiが無視できない場合、このやりかたでは測定のたびに異なる係数が得られてf(x)がiに依存しない、とは言えない結果になる。
という、普通の(式と変数の数が一致した)連立1次方程式として解くことができる(もちろん関数列の選び方によっては解けない場合もある)。例えば2点のデータで式-6の係数を決めるというような場合で、これはその2点を結ぶ直線が得られる。しかし測定の際のϵiが無視できない場合、このやりかたでは測定のたびに異なる係数が得られてf(x)がiに依存しない、とは言えない結果になる。
従ってなるべくϵiの影響を減らして安定したf(x)を得たい。そのためには測定の回数を増やす、つまりmを大きくすれば、測定ごとに変わらないf(x)が相対的に重みを増してくるだろうと考えられる。例えばひとつのx0に対して繰り返し測定をすれば平均値としてのf(x0)の確度が増すはずである。そうだとしてxiの刻みを細かくしていってたくさん測定したとして、さっきと同じことをしてみると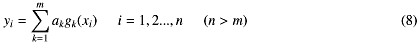 という連立1次方程式になって、これはいわゆる変数の個数mより式の数nの方が多い方程式で、一般的には解が無い。これではあまりに融通が利かないので、関数f(x)がなるべく測定値に近くなるように係数を決めるということにする。
という連立1次方程式になって、これはいわゆる変数の個数mより式の数nの方が多い方程式で、一般的には解が無い。これではあまりに融通が利かないので、関数f(x)がなるべく測定値に近くなるように係数を決めるということにする。
「なるべく近い」というのを数学的に表現するのは、いろいろな考え方があってなかなか難しいけど、たとえば誤差の2乗和 を考える。今考えている測定値は実数で、このJの項は2乗しているのでJそのものは正の数の足し算になる。従って
を考える。今考えている測定値は実数で、このJの項は2乗しているのでJそのものは正の数の足し算になる。従って
 のはずである。最初に書いたようにϵiを知る手段はないので、Jを最小にする係数の組akを決めればそれは「なるべく近い」関数になっていると考えていいだろう。誤差の2乗の和を最小にすることで係数を決めるのでこの考え方を最小2乗法という。
のはずである。最初に書いたようにϵiを知る手段はないので、Jを最小にする係数の組akを決めればそれは「なるべく近い」関数になっていると考えていいだろう。誤差の2乗の和を最小にすることで係数を決めるのでこの考え方を最小2乗法という。
ちなみにこれ以外考え方によって「なるべく近い」関数を選ぶ方法もありえる。例えば2乗のかわりに絶対値を使ってもいい。しかしϵiが正規分布になっているというのが比較的ありえることだとすると、2乗をとるということはつじつまが合っていると言える。その「つじつま」とはどういうことかというのは正規分布の不思議さが関連するけど、それはまた今度にする。
式-9のJは和の記号がごちゃごちゃしてわかりにくいけど、じっくり見ればわかるように係数akの2次式の和になっているので、それぞれの係数に関して とすれば、これを満たすakの組のときJは最小値のはずである。この場合式の数も変数の数もm個なのでちゃとひとつ解が求まることになる。
とすれば、これを満たすakの組のときJは最小値のはずである。この場合式の数も変数の数もm個なのでちゃとひとつ解が求まることになる。
もう少し中身をちゃんと書いて微分を実行すると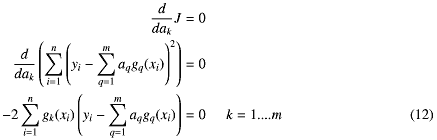 となるので結局
となるので結局
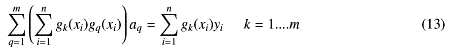 となる。ただし和の記号は順番を入れ替えて整理した。
となる。ただし和の記号は順番を入れ替えて整理した。
いっぱい書いたのでちょっと一休み。あともうちょっと普通の話が続く。
3 係数をどうやって決めるか
もしϵiが無視できるくらい小さければ、n=m、つまり測定値の数と係数の数を一致させて、従ってなるべくϵiの影響を減らして安定したf(x)を得たい。そのためには測定の回数を増やす、つまりmを大きくすれば、測定ごとに変わらないf(x)が相対的に重みを増してくるだろうと考えられる。例えばひとつのx0に対して繰り返し測定をすれば平均値としてのf(x0)の確度が増すはずである。そうだとしてxiの刻みを細かくしていってたくさん測定したとして、さっきと同じことをしてみると
「なるべく近い」というのを数学的に表現するのは、いろいろな考え方があってなかなか難しいけど、たとえば誤差の2乗和
ちなみにこれ以外考え方によって「なるべく近い」関数を選ぶ方法もありえる。例えば2乗のかわりに絶対値を使ってもいい。しかしϵiが正規分布になっているというのが比較的ありえることだとすると、2乗をとるということはつじつまが合っていると言える。その「つじつま」とはどういうことかというのは正規分布の不思議さが関連するけど、それはまた今度にする。
式-9のJは和の記号がごちゃごちゃしてわかりにくいけど、じっくり見ればわかるように係数akの2次式の和になっているので、それぞれの係数に関して
もう少し中身をちゃんと書いて微分を実行すると
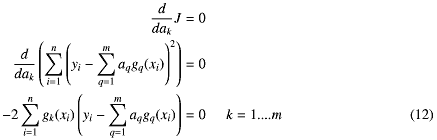
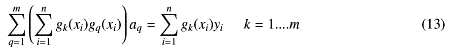
いっぱい書いたのでちょっと一休み。あともうちょっと普通の話が続く。
2013-11-19 22:14
nice!(0)
コメント(0)
トラックバック(0)


コメント 0