Bezier曲線による関数の近似 - その2

急に思いついてやり始めたBezier曲線を関数近似として使う話。サクサク行きたい．．．．

前回の式-7と式-9の解を探す前に少し特殊な例を考えてウォーミングアップする。

直接解ける例として、この図のような4分の1円を近似することを考える。これはまえにちょっとやった。あのときは1次の微係数まで合わせて、そのあとは誤差最小とした。

今回は端点での1次と2次の微係数を合わせるという方針だとどうなるかやってみる。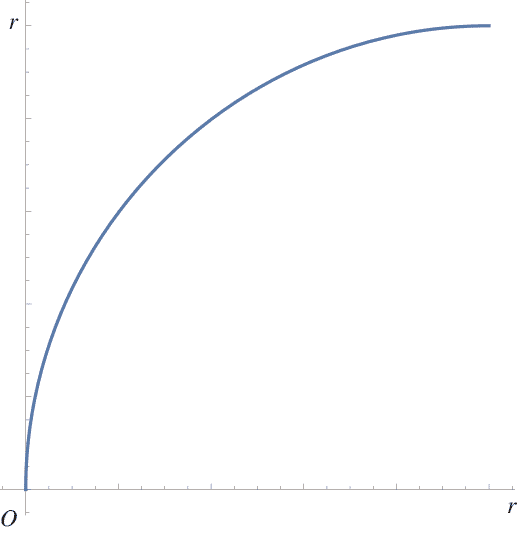

左下の端点を原点、右上の端点は座標$(r,r)$とすると、それぞれの端点での1階微分の値から \begin{align} \left. \frac{dx}{dy} \right|_{t=0} = \left. 1/\frac{dy}{dx} \right|_{t=0} &= 0 \\ \left. \frac{dy}{dx} \right|_{t=1} &= 0 \end{align} この原点での$x$に関する1階微分は発散するので、最初に限定した関数の範疇ではない。しかしこの場合は簡単なのでこのまま進める。

媒介変数の2階微分は \begin{equation} \frac{d^2x}{dy^2} = \frac{d}{dt}\left(\frac{dx}{dy}\right) / \frac{dy}{dt} \end{equation} だというのは確か前やった。

円の座標に並行な位置での座標に関する端点での2階微分の値は$1/r$だけど、符号に注意して \begin{align} \left. \frac{d^2x}{dy^2} \right|_{t=0} &= \frac{1}{r} \\ \left. \frac{d^2y}{dx^2} \right|_{t=1} &= -\frac{1}{r} \end{align} これらに前回導いた微係数の式に代入すると \begin{align} \frac{x_1}{y_1} &= 0 \\ \frac{y_2 - r}{x_2 - r} &= 0 \\ \frac{x_1y_2}{y_1}+\frac{3y_1^2}{r}-2x_2 &= 0 \\ \frac{2\left(r(x_2-x_1+y_1-y_2)-x_2y_1+x_1y_2 \right)}{3(r-x_2)^3}+\frac{1}{r} &= 0 \end{align} これを$x_1$、$x_2$、$y_1$、$y_2$について解くと \begin{equation} \begin{array}{rl} x_1 &= 0 \\ y_1 &= \displaystyle \frac{r(\sqrt{7}-1)}{3} \\ x_2 &= \displaystyle \frac{r(\sqrt{7}-1)}{3} \\ y_2 &= r \end{array} \end{equation} と簡単に解けるので、始点が原点の4分の1円を近似するBezier曲線を書き下すと \begin{align} \Big(x(t),y(t) \Big) =& \Big(r\left((4-\sqrt{7}) (1 - t) t^2 + t^3 \right), \nonumber \\ &\hspace{3mm} r \left((1-\sqrt{7}) (1 - t)^2 t + 3 (1 - t) t^2 + t^3 \right) \Big) \end{align} 真円からの誤差を知るために中心からの距離の$r$との差を$t$についてプロットしたのが

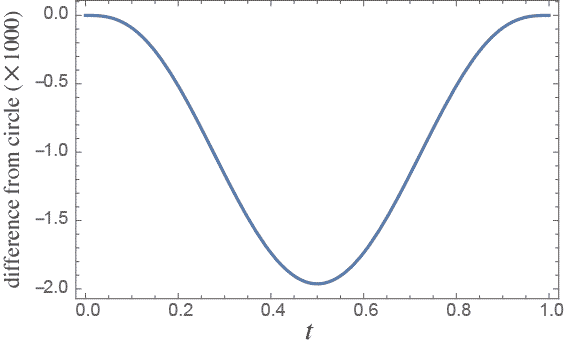$t=1/2$で0.2%ほど半径が短くなっている、ということらしい。ここでは端点での2次までの微係数を一致させたけど、誤差最小にすればさらに半分近くにはできる、というのが以前やったときの結論。しかし微係数を合わす方が数字もスッキリしている。描画のためならもうどっちでもいいということになる。

前も書いたかもしれないけど、IllustratorやmacOSのNSBezierPathやSwiftUIのPathにある「円」がどうなってるか知らないが、少なくともこれと同程度には「円」ではない。

また一旦、ここまでできればBezier曲線のAffine不変性のおかげで、4つ繋いで真円にすることができる。Illustratorで「円」を書くとアンカーポイントが4つ含まれているけど、おそらくこれでできてるんだろう。

しかし、Illustratorで円を一個描いたepsファイルが1.3MBにもなるので中を見る気はしないわ。