PWM+ローパスで擬似D/A - その3 [Pi Pico]
PWMの波形を工夫してローパスの半田付けを怠けようという話の続き。コメントでもらったジッタを与えるアルゴリズムは面白くて有効そうなんだけど、案外難しい。その前に何がしたかったか、をもういっぺんまとめると例えばの話、この絵のように
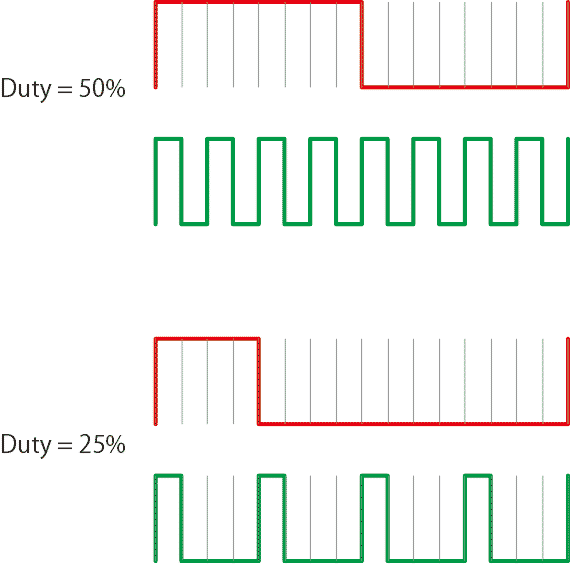 普通のPWMのデューティ比50%、というかつまり時間に沿った方向に対する1の出現確率が50%だと上の赤線のような信号波形になる。しかしその下の緑線のようにクロックごとに反転してやるとクロック周波数の半分の成分以下はなくなって、原理的に基本波成分は0である。デューティ比25%でも図の下のようにしてやれば最低の周波数成分はクロックの1/4、もとの基本波の4倍になる。
普通のPWMのデューティ比50%、というかつまり時間に沿った方向に対する1の出現確率が50%だと上の赤線のような信号波形になる。しかしその下の緑線のようにクロックごとに反転してやるとクロック周波数の半分の成分以下はなくなって、原理的に基本波成分は0である。デューティ比25%でも図の下のようにしてやれば最低の周波数成分はクロックの1/4、もとの基本波の4倍になる。
wrapの値をちょうど割り切るようなディユーティ比の場合、例えばwrapの値が16だと、2と4の場合に基本波成分は原理的に0になるけど、それ以外は基本波成分は必ず残る。それでもできればなるべく基本波成分が少ないほうがいい。
1周期の中になるべくたくさんの反転を入れてやれば同じデューティ比で(同じ0と1の比率で)基本波成分を減らすことができて、基本波より高い(クロックに近い)方へ高調波のエネルギーを寄せることができる。そしてローパスの半田付けは楽になる(1次で済ます)はずである、という話。前回は整理するための記号を作って終わってしまったのでそれを使ってどういうパターンがあり得るか考える....
ただし、これでは$n>w/2$ではPWMと同じになってしまう。でもデューティ比50%を超えたら$100-r$($r>50$)%のパターンを反転すればいい。つまり$W[w:n]$の1と0を入れ替えたパターンを$\widetilde{W}[w:n]$と書くと \begin{equation} W[w:n] = \widetilde{W}[w:w-n] \hspace{4mm}\mbox{for }n>w/2 \end{equation} とすればいい。この式-\ref{w0}を一番簡単ということで$W_0[w:n]$としておく。
簡単な場合を具体的に書いてみる。$w=16$で$n=1... 6$のパターンを波形として描いたのがこの絵である。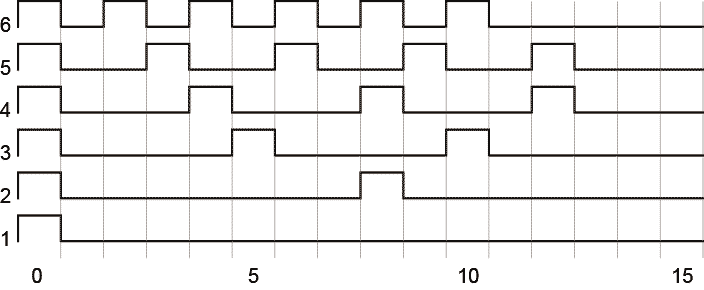 一眼見てわかるように、ちょうど割り切れる2、4の場合はうまいぐあいに収まってるけど、それ以外は後ろの0が長くなる。これは当然でそこにあまった$q-p$個の0を集めたから。
一眼見てわかるように、ちょうど割り切れる2、4の場合はうまいぐあいに収まってるけど、それ以外は後ろの0が長くなる。これは当然でそこにあまった$q-p$個の0を集めたから。
これでも普通のPWMより基本波成分は減るはず。しかしこれはいかにもナイーブに見える。
例えば余った0を$R(p)$にひとつずつ足してやればいい。つまり \begin{align} W[w:n] &= R(p+1)^rR(p)^{n-r} \\ p &= \left \lfloor w/n \right \rfloor \nonumber \\ r &= w - n p \nonumber \end{align} とする。なんか式で書いた方がかえってわかりにくくなったかもしれない。つまり上の式の$r$は余った0の数である。それを最初の$r$個の$R(p)$にくっつけて$R(p+1)$にする。残りはそのまま$R(p)$にするとちょうど1周期分になる。
これもさっきと同じように$w=16$で$n=1 ... 6$までの波形を描いてみると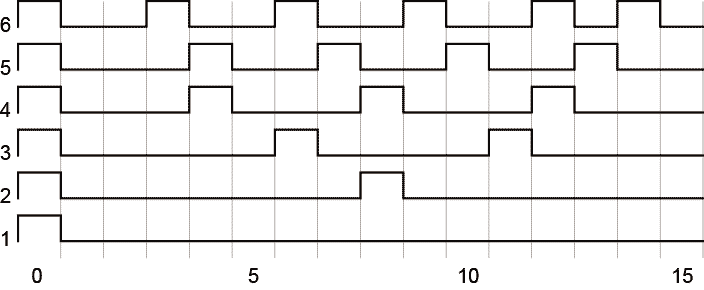 となる。$W_0[w:n]$よりは均等に近くなった。とりあえずこれを$W_1[w:n]$としておく。
となる。$W_0[w:n]$よりは均等に近くなった。とりあえずこれを$W_1[w:n]$としておく。
けど、こんどは$n=5$や$n=6$をみるとなんとなく後ろに詰まっているように見える。それはそうだよな、余った0を前のほうにくっつけたんだから。0をくっつけるブロックを1周期の中にバラまかないといけない。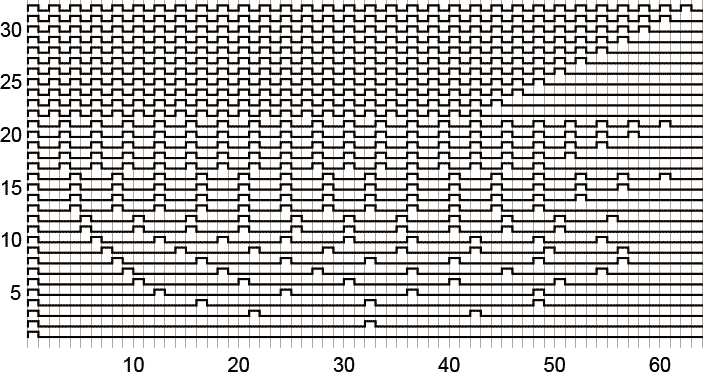 で、これが$W_1[64:n]$
で、これが$W_1[64:n]$
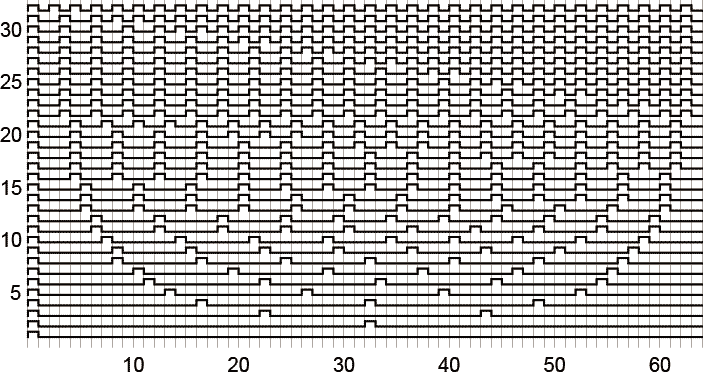 である。こうやってみると、$W_0[64:n]$は$n$が増えていくと$n>21$では普通のPWMを$R(2)$で埋めたパターンになってしまっている。それはさっきからわかっていたけど全体的に前のめりになっていることがわかる。
である。こうやってみると、$W_0[64:n]$は$n$が増えていくと$n>21$では普通のPWMを$R(2)$で埋めたパターンになってしまっている。それはさっきからわかっていたけど全体的に前のめりになっていることがわかる。
逆に$W_1[64:n]$は後ろ側に寄っている。まあそれは0を前の方に継ぎ足したからそうなったわけで、後ろに継ぎ足せば左右反転した形になる。
$W_0[64:n]$よりは$W_1[64:n]$のほうがマシ(基本波成分は少ない)のように見えるけど、やはりイマイチである。
もう少し考えてみることにする。

wrapの値をちょうど割り切るようなディユーティ比の場合、例えばwrapの値が16だと、2と4の場合に基本波成分は原理的に0になるけど、それ以外は基本波成分は必ず残る。それでもできればなるべく基本波成分が少ないほうがいい。
1周期の中になるべくたくさんの反転を入れてやれば同じデューティ比で(同じ0と1の比率で)基本波成分を減らすことができて、基本波より高い(クロックに近い)方へ高調波のエネルギーを寄せることができる。そしてローパスの半田付けは楽になる(1次で済ます)はずである、という話。前回は整理するための記号を作って終わってしまったのでそれを使ってどういうパターンがあり得るか考える....
2.2 いちばん簡単な場合
前回の記号を使って、さっきの「1」をなるべく孤立させてその間に「0」を埋めると言う思いつきを表してみると \begin{align} W[w:n] &= R(p)^{n-1}R(q) \label{w0} \\ p &= \left\lfloor \frac{w}{n} \right\rfloor \nonumber \\ q &= w-p(n-1) \nonumber \end{align} と書くことができる。ここで$\lfloor x \rfloor$はfloor関数で$x$を超えない整数を表す。つまり$p$は$w/n$の整数部分を表すことになる。$q$は$w/n$が割り切れなかった場合の辻褄合わせで、必ず$p \le q < 2p$である。ただし、これでは$n>w/2$ではPWMと同じになってしまう。でもデューティ比50%を超えたら$100-r$($r>50$)%のパターンを反転すればいい。つまり$W[w:n]$の1と0を入れ替えたパターンを$\widetilde{W}[w:n]$と書くと \begin{equation} W[w:n] = \widetilde{W}[w:w-n] \hspace{4mm}\mbox{for }n>w/2 \end{equation} とすればいい。この式-\ref{w0}を一番簡単ということで$W_0[w:n]$としておく。
簡単な場合を具体的に書いてみる。$w=16$で$n=1... 6$のパターンを波形として描いたのがこの絵である。

これでも普通のPWMより基本波成分は減るはず。しかしこれはいかにもナイーブに見える。
2.3 もう少し頭を使う
$W_0[w:n]$は余った0を全部後ろにまとめてしまったので、いつもまんべんなく1が現れるようにはなっていなかった。だとすると余った0を前の方にバラまけばいいじゃん、と思いつく。例えば余った0を$R(p)$にひとつずつ足してやればいい。つまり \begin{align} W[w:n] &= R(p+1)^rR(p)^{n-r} \\ p &= \left \lfloor w/n \right \rfloor \nonumber \\ r &= w - n p \nonumber \end{align} とする。なんか式で書いた方がかえってわかりにくくなったかもしれない。つまり上の式の$r$は余った0の数である。それを最初の$r$個の$R(p)$にくっつけて$R(p+1)$にする。残りはそのまま$R(p)$にするとちょうど1周期分になる。
これもさっきと同じように$w=16$で$n=1 ... 6$までの波形を描いてみると

けど、こんどは$n=5$や$n=6$をみるとなんとなく後ろに詰まっているように見える。それはそうだよな、余った0を前のほうにくっつけたんだから。0をくっつけるブロックを1周期の中にバラまかないといけない。
2.4 分布の様子
あまり短い$w$だとわからないので少し長くしてみてみよう。しかしあまり長くすると細かくなりすぎてやっぱりよくわからない。とりあえず$w=64$で$n=1 ... 32$として描いてみると これが$W_0[64:n]$

逆に$W_1[64:n]$は後ろ側に寄っている。まあそれは0を前の方に継ぎ足したからそうなったわけで、後ろに継ぎ足せば左右反転した形になる。
$W_0[64:n]$よりは$W_1[64:n]$のほうがマシ(基本波成分は少ない)のように見えるけど、やはりイマイチである。
もう少し考えてみることにする。
2021-11-07 21:17
nice!(0)
コメント(6)


raspberry piのハードウェアPWMにあるbalanced modeみたいな感じですね。
by boochow (2021-11-07 22:08)
コメントありがとうございます。
これはぜんぜん知りませんでした。本家Raspberry PiのPWMにはあるんですね。Raspberry PiのPWMで擬似DAをやったことがなかったので感知していませんでした。コメントいただいて初めて知りました。まったくお恥ずかしい話です。
このRaspberry Piのアルゴリズムを書いたものってどこかにあるんでしょうか。
それにPi Picoにはないんでしょうか。こっちのマニュアルは読みやすいので見直したのですが、それらしい記述は見当たりません...
by decafish (2021-11-08 18:35)
こちらで触れられているのでご存じと思っていました。
https://decafish.blog.ss-blog.jp/2015-08-28
BCM2835のマニュアルのP139に解説があります。
動作の様子はこんな感じです
https://www.youtube.com/watch?v=Ve0yn-e7d68
PicoのPWMは単純なタイマーなので、このモードは無かったと思います。検討されているようなアルゴリズムを使うのであれば、PicoのInterpolatorが役に立つかもしれません。
by boochow (2021-11-10 18:49)
うわあ、これはますます恥ずかしいです。2835ライブラリにはあったのですね。でもこれを書いている様子からこの時点ではちゃんと理解していなかったようです。
2835ライブラリからpigpioに乗り換えて、pigpioではこのモードをサポートしてなかったみたいで完全に忘れていました。最近はPi Picoばっかりだったのでさらに忘れていました。Picoにはこのモードはやはりないのですね。
マニュアルの記述見ました。ありがとうございます。やろうとしていたことはこの通りです。ただしこれだとM/N割り切れない場合、低い周波数成分、つまりMとNの最小公倍数の周期の成分が現れるような気がします。Mが大きければアナログ成分としては小さいとは思いますが。
間違っていたらごめんなさい、またご指摘ください。
by decafish (2021-11-10 19:46)
極端な例としてM=1でNをどんどん大きくしていったら、1のあとに0がN-1回続くので、周期Nの信号と見えるのは仕方ないと思います。
PWMは本来この周期よりずっと下のところでLPFをかけるわけですが、今回はLPFを簡略化するというお題なので、Nに上限を設けて(周期の下限を固定して)、その分、DAの精度をあきらめるということではないでしょうか?
by boochow (2021-11-10 21:35)
それはそうですね。
分解能と帯域がトレードオフになるのはPWMを使う限り同じのはずです。
もう一度何がしたいのか整理しないといけないです。
by decafish (2021-11-11 18:45)