太さの変わるBezier曲線の生成 - その17

仕事が忙しくてなかなか進まない。Bezier曲線で一般の曲線を近似する問題。

前回曲線の近さの都合のいい定義を与えるために、近似対象の曲線から垂直に引いた線のBezier曲線との交点までの長さの曲線に沿って積分した値を「距離」とみなした。これを最小化することで近似を得ようと考えた。近似対象の曲線が媒介変数で表わされていて、微分可能ならこの積分は（少なくとも数値的には）実行可能であることがわかった。またこれなら面倒な場合分けをする必要もなく、安定（安定性の検証はしてないけど、まあ問題ないでしょ。積分だし）。今日はこの続き。

Bezier曲線による近似の具体的計算

Q(r)を近似対象の曲線、P(t)を近似させたい3次のBezier曲線であるとする。媒介変数rとtの定義域は両方とも[0,1]であるとする。

Bezier曲線P(t)は4つの制御点

を持っているとする。

まず、

とすれば、始点と終点は簡単に一致させることができる。

また、端点での1次の微係数を一致させると

すなわち

である。ここでαとβは決定すべき未定係数である。

ここまでで、図-39のような感じ（Illustratorで直感的にやってる感じで）になる。

結局Bezier曲線P(t)の制御点は

となって、曲線Q(r)へのP(t)の近似というのはΔを最小にするαとβのふたつの係数を決める問題になる。

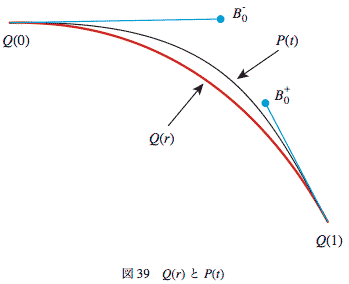
ようするに、ふたつの中間の制御点は、端点からの方向が決まっていてその端点からの距離を調節して最も近くなるような位置を探せばよいということになる。

ふたつの自由度しかないので、できることはそれほどない。

ふたつの係数の値を決める数値計算ではΔもまじめに積分する必要はなく、代表的な数点でのδの値を足すぐらいで十分であろう。つまり

としても問題ないだろう。

その代表点が1点では係数がひとつに決まらない場合もある。また、2点ではたまたまうまく2点を通るBezier曲線があり得たりするとその他の点で全然違う曲線になったりする。代表点の数は3点以上がいいだろう。本来ならいちばんふたつの曲線が離れる点を代表点に使うのがいいけど、それを探すためにまた面倒なことになる。実行効率も考えて実装するときに代表点の個数を決めることになるだろう。

Δの収束判定には、線幅を利用するのがよいと思われる。例えば

を満たせば収束したと見なすことにする。ただし、dはもとの曲線の線幅、nは代表点の個数、κは適当な係数である。代表点での距離が線幅に比べてある程度小さくなれば十分であると判断する。κはたとえば0.1などにすると距離の平均が線幅の10分の1になればOKということである。

また、Δを最小にする繰り返し計算は前にも出した非線形の最適化法が使える。ただし、たいていのアルゴリズムは微係数を要求する。今回δのαとβに関する微係数を求めることは困難である。従って微係数を必要としないNelder-Mead法などを使う必要があるが、

1. パラメータが二つしかない
2. 媒介変数tに関してたかだか3次

なので、この問題に適した最適化手法があり得ると思われる。これ以上は数学の問題ではなく実装の問題に近くなるので、実装の段階でもう一度考えなおすことにする。

次回はαとβを選んでも十分に近くならない、つまり式-123を満足することができない場合、どうするかを考える。