景品を頂いた

先日の円錐の交差の話のおかげで川合工房さんから景品を頂いた。紙の持つテクスチャ、鋏のシャープな裁ち線、そしてなりより造形が美しい。現物の写真を撮った。携帯カメラの写真ではその美しさは伝わりにくいかもしれないけど。

頂いたのは3点。

実は青い枠で囲った左の「竜騎兵」がすごいんだけど、これは未発表作品とのことなのでここでは控えさせていただく。非常に残念。

開いて平面に戻して見ると、どれも一枚の紙を切っただけの、数学で言えば連結な平面図形（右の兎を除く二つはなんと多重連結）になっている。しかし、非常に繊細な構造をしていて立体からはとても平面展開した図形を思い浮かべることができない。どうやって設計するのか全然わからない。 こういうところでは僕には全く勝ち目がないことがよくわかった。もちろん、勝ち負けではないけど。

ということで、川合工房さんの問題の一般論について。

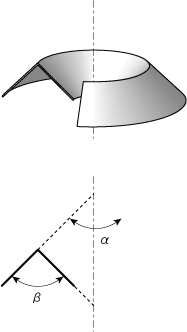図のように途中で折りを反転させた円錐の断面を考えると、図の下の絵のようになる。上下がひっくりかえった円錐の重なりと考えられるので、問題の角度は図中のβで、これは円錐の頂角のαに等しいことがわかる。αは展開したもとの扇型の開き角だけで決まる。

ところで僕の問題に対する解答は、

となる。ここで(R(θ), θ)は展開した平面上の扇型の中心の方向θとそこからの距離R(θ)の関係で、平面上の曲線を表す。 式中のdはふたつの円錐の頂点間の軸方向の距離、aは円錐の尖り具合、sはふたつの円錐の軸の距離である。

誰か気になる人がいれば、もうちょっと詳しく解説するけど、まあいいか。ふたつの円錐の軸が平行の場合は、空間図形が楕円なのでこういった適当な媒介変数を選ぶことで簡単に表せる。平行でなくなると突如として解析的に表現できなくなって楕円積分が現れる。可展面どうしの交線を平面に展開した場合、楕円積分は「またお前か」というぐらいしょっちゅう出てきておなじみになる。

「右は幾何千畳とも知れぬ深〜い谷、左は幾何千畳とも知れぬ高〜い山、その間を細〜い道が続いております」その細い道が解析関数の世界のすべて。

コメント 3

　ご紹介いただきありがとうございます。
　数式、私の理解できる数学の範囲を超えております。高校が理数科だったこともあって数学は好きなのですが、何一つ答えに近づけませんでした。でも前回記述いただいた文章だけですでに参考になるものがありまして、その辺はブログに使わせていただきます。可能を説明するには実例があればいいが、不可能を証明するには学問がいりますね。

＞「右は幾何千畳とも知れぬ深〜い谷、左は幾何千畳とも知れぬ高〜い山、その間を細〜い道が続いております」その細い道が解析関数の世界のすべて。
by 川合工房 (2010-03-04 23:54) 

その細い道を探し出して、基本的な型を作るのが私のテーマです。基本を組み合わせて作品を設計するわけです。型を覚えれば設計法の理解も比較的簡単と思います(そしてその裏を書いて不思議勘を高めていく）。

　ＰＳ　竜騎兵は公開いただいてまったく構いません。
by 川合工房 (2010-03-05 00:08) 

コメントありがとうございます。
数学は便利な道具ですがその限界は意外なところにすぐ顔を出します。ペーパークラフトの数学はまさにその典型です。
僕の場合、数学の限界は僕自身の限界に一致してしまってそれを超えることが難しくなっています。
川合工房さんがかるがるとそれを超えてしまわれるので、僕としてはその限界の中にもある数学の美しさを強調したいと思っています。が、なかなか難しいです。
by decafish (2010-03-05 21:57)