厳密な光線追跡 - その7

前回までで光学に出てくる面形状に光線が入射するとき、その光線と面との交点を求めた。解が解析的に書けると繰り返しの収束演算をする必要がなくて速い。また収束演算が必要な場合でも、解析解を初期値に使えるような面形状だと収束は速いし、収束も安定になることが期待できる。

今日はちょっと横道にそれるけど、それにまつわる数値計算精度の話。

先に言っておくけど、僕はここで「精度が低下するぞ、恐ろしいぞ」と脅かすつもりはない。若い人はどんどんいろんなことをやって痛い目にあえばいい。それが勉強だし僕も痛い目にあってきた。僕が言いたいのは、光学の大家に相談したとき「自由度が足りないなら奇数次を入れれば？」と言われてえらい人の言うことだから、と思考停止的に鵜呑みにするのは危険である、ということ。

光学は古い分野で年寄りがいつまでものさばっている、と僕は思っている。僕が若い人に伝えたいのは、年寄りが「奇数次」と言ったときに、ちょっと待てよ、と思ってほしいということである。

3.3.5  ベキ項での桁落ちの発生

ここでちょっと非球面式を使う上での計算精度の問題についてさらっとまとめておく。

10次以上を使ったり高次の係数が大きかったり、また外周部で微係数の符号が入れ替わったりしていると収束が悪くなったり精度が足りずに桁落ちしたり、と言う問題が起こることが多い。特に最適化の過程でベキの係数を最適化パラメータに選んだりすると発生する場合がある。CodeVなどはそのへんにノウハウが生かされていて、自動的に素性の悪い途中解を排除するようになっていたりするらしい。

具体的に言えば、例えば半径5mmのレンズの面を非球面式で表現することを考える。

ベキの項の付加によって何ミリもサグ（面の深さ）をとることは通常はありえない。普通は波長のオーダからそのひと桁ふた桁大きい程度である。

そして非常に高次まで、例えば20次までとることを考える。つまり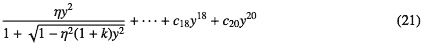

としたとする。レンズの端（r ≈ 5）のとことでy¹⁸は十進で13桁、y²⁰はほとんど15桁の数になる。 c₁₈やc₂₀が10⁻¹⁵から10⁻¹⁷ぐらいの非常に小さな数ならとりあえず問題はない（ベキ数の計算精度は桁落ちが考慮されているとして）。

しかしこのふたつの係数が異符号どうしで、絶対値がこれより大きい場合はかならず桁落ちが起こっていると判断してまちがいない。となりあう係数の符号が逆になることは非常によくある。これはあとで例を示す。

普通のハードウェアが持っている浮動小数点演算ユニットはdouble幅で16桁の精度（2進で52桁）を持っている。例えば極端な場合として係数が1のオーダを持った逆符号の数だったとしよう。これで波長のオーダを表現した場合2〜3桁程度の有効数字しかないということになる。

またここで、光学系の光路長を計算することを考える。物体から像面まで（あるいは物体を中心とした入射瞳上の球面から近軸像点を中心とした射出瞳上の球面まで）の光路長の総和は、幾何光学的な光線から波面収差、回折などを計算するときの橋渡しとなる。

例えば写真レンズの場合などでは光路長はおおよそレンズ全長のオーダ、100mmぐらいになる。それから波面収差を計算するためには波長の百分の一以下、つまりnm以下の光路長差を計算することになる。この時点で自動的に有効桁は8桁程度に劣化する。

その途中にさきほどの桁落ちした非球面が含まれていると、光路長の有効桁はさらに低下する。

まあ、ほんとうにこれは極端な例で、写真レンズで回折限界を要求することはあまりないとは思うけど、こういうところにもセンスは必要である。

3.3.6  ベキ関数で表現できる限界

もうすこし非球面式の計算精度について、精度が確保しやすい場合とそうでない場合について具体的にみてみる。

非球面式のベキ項を付加することで2次曲面とは異なる面形状を表現できる。 しかしベキ項が得意な形状とそうでない形状がある。

例えば

を±1の範囲で数値化して（均等な刻みで201ポイント）、10次までのベキ関数で最小2乗フィットしてみると

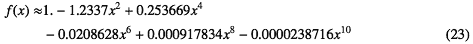となる。これは

とテイラー展開できることからもわかる。

このベキ展開の元関数との差分は図-1のようになる。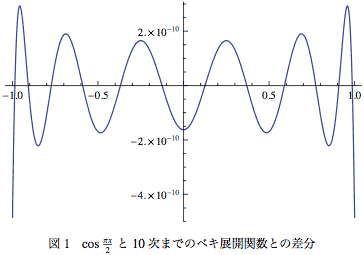

おおよそ10⁻⁹の差しかないことがわかる。

ところがこんどは

を同じように展開してみると

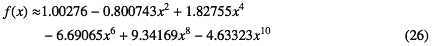となって、式-23と較べれば大きな次数の係数が十分に小さくないことがわかる。同じように差分をプロットしてみると図-2のようになって、図-1と較べると8桁近く悪いということがわかる。

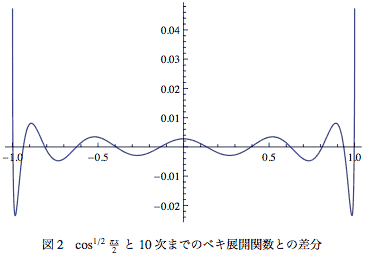つまり、ベキ級数には得手不得手があるということである。面形状はその問題に内在する特性に依存していて、非球面式で表現できるかどうかとは別問題である。つまりcosπx/2のような形状が必要となるか、cos^1/2 πx/2のような形状になるかは問題そのものに依存している。

また、式-26を見ると隣り合う次数の係数の符号が逆になっている。これは最小2乗で係数を求めているためで残差の2乗の和を細小にしようとすると必然的にこうなる（フィットした関数がもとの関数のまわりに行ったり来たりすれば2乗和を小さくできる）。

これは極端な例ではあるけど、桁落ちの発生する典型的な例である。非球面式の限界と危険性はこういうところにある。

ちなみにcos^1/2 πx/2を、同じやり方で奇数次も含めたベキでフィットすると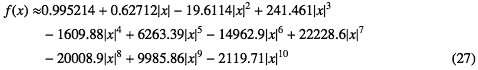

となって、残差は図-3のようになる。

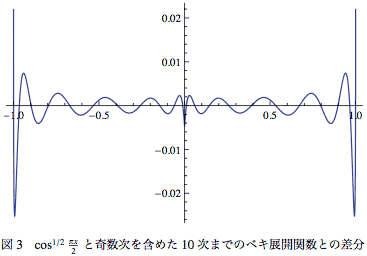項の数は倍になっているのに残差の大きさは半分程度にしかなっていない。そして次数が高くなるほど係数の絶対値は大きくなっていく。そしてまるで作ったように符号がかわりばんこになっている。そして、とくに原点付近をよく見て欲しい。ヘソみたいな滑らかでないエラーが発生している。これは絶対値の素性の悪さ（微分不可能性）が現れた結果である。

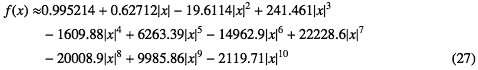
これは代表点の選び方（光線の飛ばし方）やその重み（光学面は回転対称な場合が多くて、周辺のほうに重くなる）によっても結果は違ってくるが、奇数次による展開は注意が必要である。

3.3.7  収束計算

収束計算にはニュートン法を使うのが一般的である。まず2次曲面（ベキ項のない式）での交点を求めて（これはまえやったように解析的に求まる）それを初期値として使う。できればニュートン法ではなくはさみうち法が使えればいいんだけど、一般的な書き方がみつからなかった。

Mathematicaでは汎用的に収束計算ができるFindRootという関数がある。これは初期値をひとつ指定するとニュートン法を使って解を求める。ふたつ指定すると「割線法の変形」を使うとマニュアルに書いてある。

「変形」というのが具体的にはなんなのかわからないけど、ニュートン法では微分を使って初期値をふたつ指定すれば微分を使わなくなるということらしい。

光学面の場合、単射の関数でしかも本質的に十分なめらかなはずなのでニュートン法で解が不安定になるということはない。しかし高次のベキは桁落ちなどで実効的な有効桁が減る可能性が高いことや、最適化の途中などで単射でなくなる、つまり違う場所が同じ値をとることがあるとニュートン法では問題が出る場合がある。こういう場合はアルゴリズムを変更するより、ニュートン法が適用可能な面だけを対象に限定すべきである、と僕は思うんだけど。

今回の光線追跡エンジンで最適化計算（設計）までやるつもりはないので、これ以上はつっこまない。しかしCodeVやZemaxを使っている人は、高次の係数を使うときに計算精度の低下が発生する可能性があることを忘れずにいる必要があると思う。