最小2乗法 - その13

最小2乗法の話はきょうでおしまい。今日の最後は、キャッチーに書けば「Householder法なんていらない」という結論。

なお、今日のを含めて記事をpdfにまとめたものをここに置いておく。また、Householder法を実装して数値実験したソースをここに置いておく。ソースの方は計算効率を考えて書いた訳ではないので、Householder法によるQR分解の具体的なアルゴリズムの参考として、Objective-C（とvDSPフレームワーク）による数値計算の実装の例として、また今日この後に示した数値実験の追試のためと考えていただきたい。コードは効率よりもObjective-Cのクラスとしての見通しの良さに注意したつもり（しかしMatrixのコードなど、見通しがいいとは言えないものになってはいるけど）。

5.3.2  誤差を含む

元のデータに誤差を含めるとどうなるかみてみる。

正規分布の誤差を発生させるために Box-Muller法を使った。近似するモデル関数の次数は10次までとった。

その結果を図-19に示す。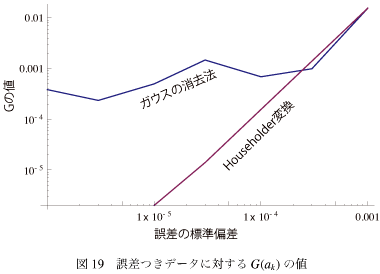

データのオーダが1程度で、誤差の標準偏差がその0.1%を超えるとガウスの消去法もHouseholder変換も同じようにあがってしまって、結果得られた係数の誤差は1%を超えてしまう。それまではガウスの消去法は高値安定で、ざっくり0.1%前後の誤差がいつも含まれるということになる。この違いが「数値的安定性の差」の具体例ということである。

ちなみに、S/Nが0.1%なんていうのは例えば光学測定では超高精度な領域で、それをクリアしようとまじめに考えたら、ハードウェアのチョッパでロックインで、ということになってしまう。そうではない普通のデータに対してQR分解にほんとうに意味があるのか、という根源的な疑問を持つのがあたりまえだろうと僕は思う。

まあそれはいいとして、グラフに帰ると、次数をかえた場合と同じようにHouseholder変換もある傾きであがっている。前回のグラフと比べると、この原因がなになのか、ということはだいたい予想がつくと思う。

5.3.3  もうひとつのやりかた

ずっと以前に近似するモデル関数をベキにするより、もっと直交性のいい関数を使って、その結果をベキに展開する、というほうが安定性はあがる、と指摘した。

その結果を見てみる。

つまりモデル関数を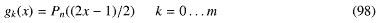

とする。P_n(x)はルジャンドルの多項式で低い次数を書き出すと

などとなっている。この多項式は区間(−1,1)で直交するので、今回の場合の(0,1)区間をこの範囲にマップして計算した後、係数を展開してベキの次数ごとにまとめる、つまりP_k(x)はx^kまでの次数しか含まないので

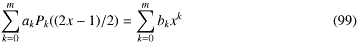としてxの係数を辺々比較してベキの係数b_kを決めればいい（と簡単に書いたけど、実際に係数を求めるのはめんどくさい。僕の場合ソースをみてもらえばわかるけどMathematicaのSplice関数を使って力づくでやった。もう少しエレガントな方法はないだろうか。ちなみにLegendre多項式そのものも20次までをハードコードしてある。double（倍精度）でも10進16桁ぐらいしか精度が無いのでどのみちそんな程度しか役に立たない。このへんが汎用の数値計算の限界）。

これを使ってガウスの消去法で係数を計算して評価関数の値を計算してみる。

例えば誤差に対する評価関数は図-20のようになる。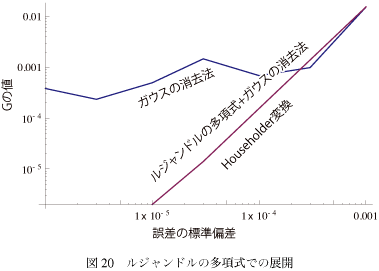

グラフを見てルジャンドルの多項式を使った線を探してしまうけど、実はHouseholder変換の値とまったく同じになってぴったりと重なっている。つまりもとのシミュレータ関数からのはずれかたまで含めて全く同じ結果になっている。

ということはすなわち、ガウスの消去法（LU分解）でもモデル関数として直行性のいい関数を使えば、数値的な安定性は劣化しない、ということがこれでわかる。すなわちモデル関数として適切なものを選べば、ガウスの消去法で十分であり、しかもその場合QR分解より計算量は少なくてすむということである。

ちなみに、ルジャンドルの多項式を使ってHouseholder変換を行っても全く同じ線になる。ということはこの線はアルゴリズムではなく、別の要素（例えば倍精度の有効数字など）で決まっていると考えていい、ということになる。

実はこの結果は正規方程式から始めても、行数の方が多い不能の方程式から始めても、結果の係数の値のふれ方まで含めてまったく同じ結果になる。重なった線を示してもしょうがないので具体的な数字はここでは出さないけど、この結果は当たり前のようで、でもなんだかすごく不思議な気もする。

今回は5次までのベキですべての係数のオーダがすべて同じでのシミュレーションだった。普通の物理現象のデータを相手にした場合、現象に含まれる次数は高次ほど係数の値は小さくなるけど、高次ほど大きなエラーをもたらす。そういう現実の係数の大きさのデコボコがベキ展開の精度に影響する。今回すべて同じ精度という結果になったけど、現実のデータに対してはそれぞれが違った精度になるということは十分にある。

たかが線形のフィッティングじゃん、というなかれ。数学を道具として使う現場では、これはこれで奥が深い。

今回は効率を気にして実装しなかったので、アルゴリズム以外の部分で効率の差が出てると判断を間違う可能性があるため実行効率の比較はしなかったが、大きな行列に対する実行効率は大きく開く可能性がある。ちゃんと実装したら比較してみたい。

ベキ展開をする必要のある人は、こういうことも研究してみてはいかがだろうか。

これも十分面白いと思うんだけど。

コメント 7

こんにちは。正規方程式の正規行列（G^T G）をLU分解するのは、コレスキー分解（R^T R）でしょうか？（cf. 最小二乗法#解法例（Wikipedia））
by zyx (2014-07-30 23:28) 

こんにちは。正しくは「正則行列（G^T G）」でした。「正規行列」と書いたのは誤りでした。
by zyx (2014-07-30 23:36) 

コメントありがとうございます。
比較のために実装したLU分解はコレスキー分解ではなく、ナイーブな掃き出し法によるものです。
コレスキー分解のほうが計算量は少ないのですが、最小2乗法を倍精度で実装してベキ展開することを考えると、桁落ちのせいでせいぜい20次ぐらいまでしか安定に計算できないので、計算効率的にはそこが律速しないと思いました。

そういえば、会社に入ったばっかりの頃にLU分解を実装したとき、計算量は半分になるはずのコレスキー分解が掃き出し法とほとんど変わらないということがありました。結局、コレスキー分解には平方根が必要ですが、掃き出し法では四則演算しかなかったというのが原因でした。当時のハードウェアではlibmのsqrt()がソフトで実装されていて、最悪の場合かけ算の数十倍の時間がかかっていました。
CPUに内蔵されたベクタユニットが倍精度の平方根を1クロックで2個計算する今となっては信じられないような昔話ですが．．．．
by decafish (2014-07-31 22:05) 

こんにちは。おっしゃる通り G^T G = L U であれば良いので、G = Q R でも良いし選択肢はいろいろですね。またどの三角化でも G 単独よりも、y とメモリ上で並べてまとめて行うとその後が簡素のようですね。
by zyx (2014-08-02 23:54) 

いくら平方根の計算が遅くても、行列のサイズが大きくなるとコレスキー分解が効率的に優位になるはずですね。でも僕は例えば1000×1000の行列のLU分解が必要になるような問題に出会ったことはありませんでした。1次の連立方程式に帰着できる数値計算問題はよくあるので、たまたまそうだった、というだけですが。

LU分解のサンプルコードを示してくれているところはいろいろあるのですが、あんがい正方行列決めうちのコードが多いような気がします。(N+1)×Nや、もっと一般のM×Nでも同じように分解できますし（三角じゃなくて台形になったりしますが）、実用上はおっしゃるように非斉次項をまとめて計算できたりするので便利だと思うのですが。
by decafish (2014-08-03 20:52) 

こんにちは。R^T D R の Cholesky 分解で三角行列を作ると平方根計算が無く良いのかもしれませんね。結局、それは対称行列を仮定したLU分解ですが。
by zyx (2014-08-08 00:30) 

平方根の出てこないコレスキー分解ってできるんですか。知りませんでした。
昔それを知っていれば、ひょっとすると効率のいい実装ができていたかもしれません。当時は結果を出すのに1ヶ月かかる、とかいうのでもなければ実行効率には無頓着でしたが．．．．
by decafish (2014-08-09 18:27)