「数学の魔術師たち」読了 [読書]
木村俊一著、角川ソフィア文庫。

前読んだ「連分数のふしぎ」の著者だった。「連分数」は面白かったしいろいろ遊んだので。この本でもひとつ遊びのネタをもらった....
数学エッセイというか数学コラムというか、数学のいろいろな分野で面白そうな話をとりあげた本。テーマは多岐にわたっていて、少なくとも「連分数のふしぎ」にくらべるとちょっと散漫、というかずっと読み物風になってる。
「はじめに」の最後に
「数学なんか、わかる必要はない。数学はわからないからこそ面白い」
と宣言している。本の腰巻の惹句では微妙に変形してるのが、かえって情けない。でも「わからないこそ面白い」と言える人はやっぱり数学が得意な人だろうと思ってしまう。数学の苦手な人がそう言われて「そんなもんか」と思って、この本を読んでもなかなか面白いと思えないのではないだろうか。でも、著者のおおらかな、あまり数学者らしくない適当さ加減は、読んでいてなんとなくホッとする。これは著者の人柄なんだろうな、と思う。
僕はどっちかというと解析は得意な方なので、カントールの話や非ユークリッド幾何学の「初歩的」な話は馴染み深かった。でも整数論は苦手なので、いくつかでてくるラマヌジャンの話はどれもちょっと読んだだけでは全然わからなかった。
例えば、
そういうのとはべつに、ちょっと試してみよう、と思えた問題がある。
ところが、この問題にはもっと簡単な解法があることを著者が種明かししてくれている。それは、交わっている2本を取り出して、結ぶ点を入れ替えて交わらないようにする。交わっているときより交わりのない場合の方が線分の長さは短いので、それを繰り返すと長さの総和はどんどん短くなって、あるところで交わりがなくなる。途中で新しい交わりができたりするけど、それも含めて交わりをなくすようにすればいい。
これは著者もプログラムを書いて計算させてみたらしい。組み合わせを網羅する場合よりもずっと短い時間で解にたどり着いたという。
面白いと思ったので、僕も書いてみた。アルゴリズムのキモとしては交点の探索が一番重要。これは普通にやれば、線分同士の総当りになる。点の数を2nとしたときにn(n-1)/2通りを探せばいいだけではあるけど、それでも多いのでどれだけ効率のいい実装ができるかで、全体のスピードが決まってしまう。
僕は最初、低解像度のビットマップを使うことを考えたけど、それはそれで結構めんどくさい。結局ごく普通に
それをOS Xのアプリにまとめた。表示ウィンドウひとつとコントロールウィンドウひとつの単純なもの。点の数を与えればランダムに表示して、かってに結んで、かってに交わった線を探して取り除いて、交わりがなくなったら終わる、というもの。点の数を指定した後は見てるしかない。ひとつの線分ペアを処理するたびに描き替えてるので、ゆっくり見られるけど、数が多くなると時間がかかるので表示をスキップするスイッチも設けた。スキップしたときは総当たり1回ごとに表示をあらためるだけになっている。詳細はソースを公開したので見て欲しい。
動かしてるところをYouTubeにあげた。
ところで、このやりかたは「どの線分も互いに交わらないようにせよ」という問題に対する解答を与える。しかし「長さの合計が最短になるような線分を求めよ」という問題には使えない。なぜなら、点の配置によっては最短でなくても交わりが無くなる場合があるからである。「最短になるような線分」は「巡回セールスマン問題」と全く同じになってしまう。
それと、動かしていて気づいたことがある。点を正方形の中にランダムに出して、そこからふたつランダムに選んで線分を引き、それを上のアルゴリズムで交わりをなくすようにすると、線分の長さの合計の短縮率(最初の長さに対する交わりがなくなったときの長さ)は、とうぜん点の数が多い方が比が小さくなりそうだ、ということはわかるけど、それがまた例によってベキに比例する。
点の数を横軸にして実際に動作させた結果の短縮率をLog Logでプロットすると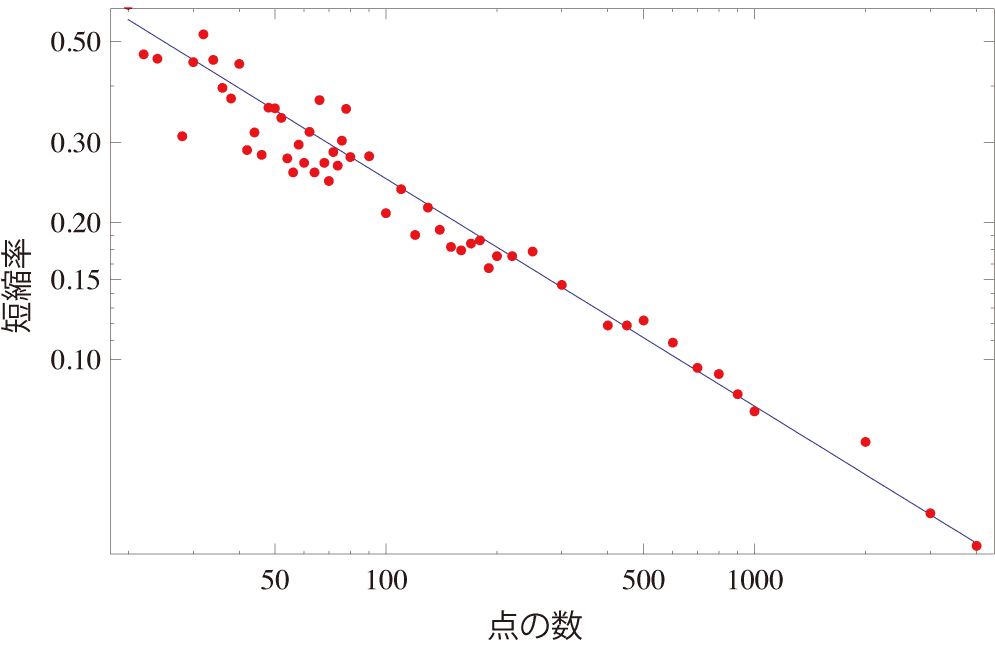 となった。直線は1/n1/2の線。-1/2乗が一番フィットするように見えた。
ベキになるのはもとがランダムだからなんとなく当たり前のような気がするんだけど、なんでそうなるかはよくわからない。それになんで-1/2乗なんだろ?不思議だ。
となった。直線は1/n1/2の線。-1/2乗が一番フィットするように見えた。
ベキになるのはもとがランダムだからなんとなく当たり前のような気がするんだけど、なんでそうなるかはよくわからない。それになんで-1/2乗なんだろ?不思議だ。
誰か教えて、偉い人。

前読んだ「連分数のふしぎ」の著者だった。「連分数」は面白かったしいろいろ遊んだので。この本でもひとつ遊びのネタをもらった....
数学エッセイというか数学コラムというか、数学のいろいろな分野で面白そうな話をとりあげた本。テーマは多岐にわたっていて、少なくとも「連分数のふしぎ」にくらべるとちょっと散漫、というかずっと読み物風になってる。
「はじめに」の最後に
「数学なんか、わかる必要はない。数学はわからないからこそ面白い」
と宣言している。本の腰巻の惹句では微妙に変形してるのが、かえって情けない。でも「わからないこそ面白い」と言える人はやっぱり数学が得意な人だろうと思ってしまう。数学の苦手な人がそう言われて「そんなもんか」と思って、この本を読んでもなかなか面白いと思えないのではないだろうか。でも、著者のおおらかな、あまり数学者らしくない適当さ加減は、読んでいてなんとなくホッとする。これは著者の人柄なんだろうな、と思う。
僕はどっちかというと解析は得意な方なので、カントールの話や非ユークリッド幾何学の「初歩的」な話は馴染み深かった。でも整数論は苦手なので、いくつかでてくるラマヌジャンの話はどれもちょっと読んだだけでは全然わからなかった。
例えば、
通りに家がずらっと並んでいて、端から順番に1番、2番...と番地番号が付けられている。さて、ある家の左側に並んている番地番号を全て足した数と右側に並んでいる番地番号を全て足した数が同じになるという。この家の番地番号は何番で、通りには家が何軒あるかという問題があった。僕は整数間の方程式までは書けたけど、それをどうやって解くのかぜんぜんわからなかった。それをラマヌジャンはある連分数をとちゅうで切った有理数がそのままその解を表すと気がついたという。本書の「付録A」にその解答があるけど、なんでそうなるのか、いったいどうやってそれにたどりついたのか、まったくわからなかった。あらためて数学の天才というのはすごい、と思った。
そういうのとはべつに、ちょっと試してみよう、と思えた問題がある。
平面上に点が偶数個ある。これらを2つずつペアにして、それぞれを線分で結ぶ。このとき、うまくペアを作れば、どの線分も互いに交わらないようにできるか?これは、試行錯誤的に探すのはけっこう大変。この本にあるように、あらゆる組み合わせの中で線分の長さの総和が最短になるものには交わりがない、ということはわかる。ところがその組み合わせを探すのは組み合わせ爆発の典型的な問題で、点の数が増えるとあっというまに検討すべきパターンの数が増えてしまう。
ところが、この問題にはもっと簡単な解法があることを著者が種明かししてくれている。それは、交わっている2本を取り出して、結ぶ点を入れ替えて交わらないようにする。交わっているときより交わりのない場合の方が線分の長さは短いので、それを繰り返すと長さの総和はどんどん短くなって、あるところで交わりがなくなる。途中で新しい交わりができたりするけど、それも含めて交わりをなくすようにすればいい。
これは著者もプログラムを書いて計算させてみたらしい。組み合わせを網羅する場合よりもずっと短い時間で解にたどり着いたという。
面白いと思ったので、僕も書いてみた。アルゴリズムのキモとしては交点の探索が一番重要。これは普通にやれば、線分同士の総当りになる。点の数を2nとしたときにn(n-1)/2通りを探せばいいだけではあるけど、それでも多いのでどれだけ効率のいい実装ができるかで、全体のスピードが決まってしまう。
僕は最初、低解像度のビットマップを使うことを考えたけど、それはそれで結構めんどくさい。結局ごく普通に
- ふたつの線分のAABB(線分を包含する軸に平行な四角形)どうしに交差がないか調べる。なければ交点はない
- AABBに交差がある場合、一方の線分から見てもう一方の線分の二つの端点が左右どちらにあるか調べる。両方が同じ側にあれば交点はない
- 両側にある場合、具体的に交点座標を求める。座標が両方の線分に含まれていればそれは交点
それをOS Xのアプリにまとめた。表示ウィンドウひとつとコントロールウィンドウひとつの単純なもの。点の数を与えればランダムに表示して、かってに結んで、かってに交わった線を探して取り除いて、交わりがなくなったら終わる、というもの。点の数を指定した後は見てるしかない。ひとつの線分ペアを処理するたびに描き替えてるので、ゆっくり見られるけど、数が多くなると時間がかかるので表示をスキップするスイッチも設けた。スキップしたときは総当たり1回ごとに表示をあらためるだけになっている。詳細はソースを公開したので見て欲しい。
動かしてるところをYouTubeにあげた。
ところで、このやりかたは「どの線分も互いに交わらないようにせよ」という問題に対する解答を与える。しかし「長さの合計が最短になるような線分を求めよ」という問題には使えない。なぜなら、点の配置によっては最短でなくても交わりが無くなる場合があるからである。「最短になるような線分」は「巡回セールスマン問題」と全く同じになってしまう。
それと、動かしていて気づいたことがある。点を正方形の中にランダムに出して、そこからふたつランダムに選んで線分を引き、それを上のアルゴリズムで交わりをなくすようにすると、線分の長さの合計の短縮率(最初の長さに対する交わりがなくなったときの長さ)は、とうぜん点の数が多い方が比が小さくなりそうだ、ということはわかるけど、それがまた例によってベキに比例する。
点の数を横軸にして実際に動作させた結果の短縮率をLog Logでプロットすると

誰か教えて、偉い人。
2015-06-02 21:27
nice!(0)
コメント(0)
トラックバック(0)


コメント 0