「ネットで話題の錯視立体」を作る（ペーパークラフトで）

実は今日は僕の誕生日でしかも還暦を迎えた。誕生日が覚えやすいので、今いる会社のみんなが「赤いちゃんちゃんこ」の「大黒頭巾」のと僕をいじる。副社長は「還暦記念パーティ」なんて言い出す。彼は僕より二つ下なので「2年後どうなるか」と脅した。

それはまあいいとして先週、流行りの錯視立体Ambiguous Cylinder Illusionが立体としてどうなっているか考えた。その結果形状の陽な表現が得られた。それはそれで面白かったんだけど、せっかく式が書き下せてるのでそれに従って実際の立体を作ってみた。でも3Dプリンタを使ったりするのはお金がかかるのでやめて紙で作ることにした。

そのためにはあとちょっとだけ計算が必要になる．．．．．

斜め45°上方向からあのように見えるような面の式は \begin{align} c_0(\theta,z)&=(-\sin \theta+\cos \theta+1,\;2 \sin \theta,\;-\sin \theta-\cos \theta+1+z)\nonumber \\ c_1(\theta,z)&=(-\sin \theta+\cos \theta-1,\;2 \cos \theta,\;\sin \theta+\cos \theta-1+z)\nonumber \\ c_2(\theta,z)&=(\sin \theta-\cos \theta-1,\;-2 \sin \theta,\;\sin \theta+\cos \theta-1+z)\nonumber \\ c_3(\theta,z)&=(\sin \theta-\cos \theta+1,\;-2 \cos \theta,\;-\sin \theta-\cos \theta+1+z)\nonumber \\ 0\le &\theta < \pi/2\nonumber \\ -1\le &z \le 1\nonumber \end{align} となった。面が4つに分かれているのは、ひし形の4つの平面と楕円柱（断面が楕円のパイプ）との交点から形状を決めたため。これらの式はもっと簡単にできるけど、これはどの面も、上から（$(0,0,1)$の方向）から見ると$\theta$が増える向きに反時計回りになっていて作るのに便利なので、このまま使う（それに従って面の順番も変えた）。$z$に残った定数項とかも簡単にしようと思えばできるけど、まあいいよ。僕は簡単化に対する情熱は数学専門の人に比べると全然熱くない。

でも、もうちょっと説明しやすい形にする。まず座標軸の名前と混同するので$z$は$h$にする。それぞれの面の式は \begin{equation} c_i(\theta,h)=(c_{ix}(\theta,h),\;c_{iy}(\theta,h),\;c_{iz}(\theta,h)) \end{equation} みたいな形をしている（添字の$i$は4つの面の一つを指定する）。つまり二つのパラメータ$\theta$と$h$で3次元の点の集合を指定していて、これは面を表すことになるのは自明である。しかしパラメータ$h$は$z$成分にしか含まれていないので、$\theta$=（一定）は$z$軸に平行な直線になる。つまり$c_i(\theta,h)$で表される曲面はいわゆる可展面（すべての点でガウス曲率が0）である。従ってペーパークラフトで作ることができる。

$c_i(\theta,h)$を平面に展開することを考える。まず展開した平面座標で$z$を同じ方向にとることにする。つまり平面座標での$z$方向は組み立てた時の3次元座標で$z$になる、ということである。平面座標でそれに垂直な座標を$w$とする。つまり展開した平面の座標は$(w,z)$とでもする。$\theta=0$の直線は当然$(w,z)$でも直線で$z$軸に平行である。ということは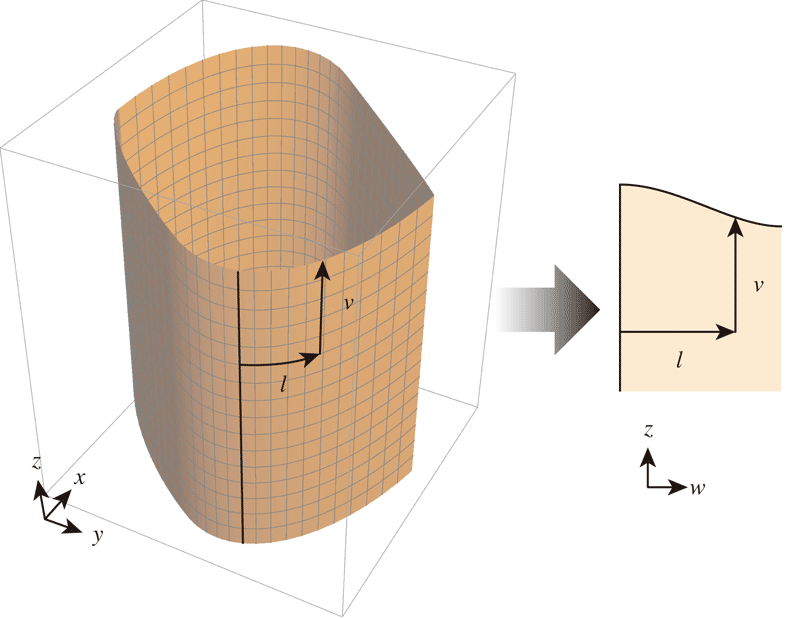

のように、$\theta=0$からの面に沿った方向の距離$\ell_i(\theta)$とそこでの立体のふちまでの高さ$v_i(\theta)$で$(w,z)$平面に描ければいいということになる。

$\ell_i(\theta)$は線積分すればいいので式-1から \begin{equation} \ell_i(\theta) = \int_0^\theta \sqrt{(\frac{d}{dt}c_{ix}(\tau,h))^2+(\frac{d}{dt}c_{iy}(\tau,h))^2} d\tau \end{equation} と書ける。$h$が残ってるように書いてしまったけど、$x$成分と$y$成分にはもともと含まれてないので関係ない。また$v_i(\theta)$の方は$z$成分そのままなので \begin{equation} v_i(\theta) = c_{iz}(\theta,h_0) \end{equation} である。ここで$h_0$は高さを決める適当な値である。

これだけではただの筒で、3次元の形状として決まらないので、筒の中に形を決める詰め物を作る。それは$(x,y,h_0)$面の断面の形が決まればいい。断面の式は簡単で \begin{equation} (x,y)=(c_{ix}(\theta,h_0),\;c_{iy}(\theta,h_0)) \end{equation} でいい。また$h_0$が含まれているように書いたけど、実際には関係ない。

これでペーパークラフトの型紙になるものはできた。あとは具体的な形状を描くだけだけど、式-2の積分がどうなるか考えないといけない。この積分の中身は例えば$c_0(\theta,h)$では \begin{equation} \int_0^\theta \sqrt{3+2\cos 2\tau+\sin 2\tau}\;d\tau \end{equation} になる。これはなんとなく簡単そうに見えるけど、初等関数では表せないらしい（Mathematicaではなんだか超幾何関数が含まれた難しい式が返ってきた）。まあ、でも滑らかなので数値積分で精度よく求まるはずである。

で、計算を実行して型紙を作ってみた。こんなになった。

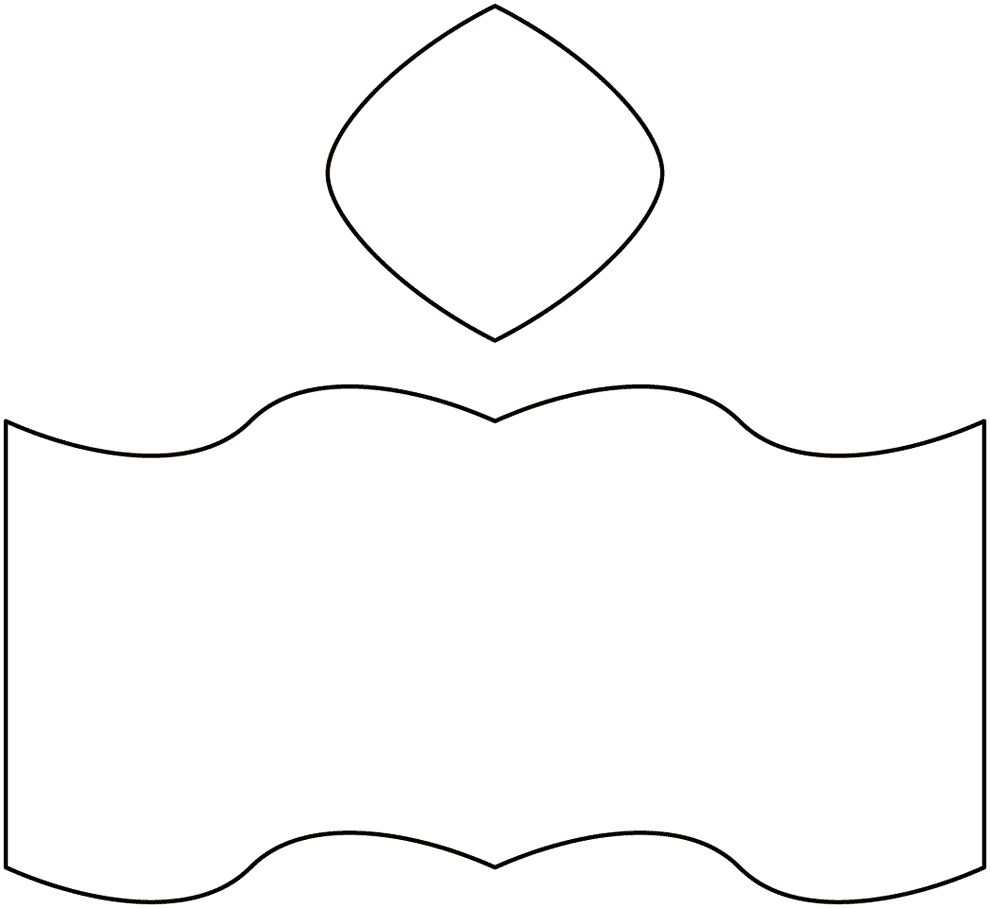
二つの閉曲線に適当にのりしろをつけて、上にある角が丸まったひし形をつっぱりにして、下にある帯みたいなのを巻きつけるとできるはずだと考えた。

でもこれを紙で作ってみるとなかなか難しいことがわかった。小さいと精度が出せなくて見た目が変になって、大きいとつっぱりが平らにならずにへろへろしてしまう。つっぱりにするのを画用紙で何枚か作って糊で貼り合わせて厚みをつけて、帯を巻き付けようとしたら、つっぱりが精度よく切り抜かれてないせいで、外形が全部の論理和になって帯の長さがぜんぜん足りなくなった。ペーパークラフトではやっぱり円錐の組み合わせのような剛性が上がって形が作りやすい。パイプのようなのは形を決めるのが難しい。

それと、作ってみて初めて気がついたんだけど、これは単独では立たない。オリジナルのムービーでは必ず格子状に複数個配置されてたのはそういう意味があったのか。なるほど。

いろいろ考えて、百円ショップで1mm厚のウレタンシートと10mm厚のポリスチレン板を買ってきた。ポリスチレンを削ってつっぱりにして、ウレタンシートを切り貼りして巻きつけた。こんなの。

ウレタンシートの厚みを考慮して、一回り小さいつっぱりを作って、ちょうど収まるように削った。鏡の前で180°回す動画も作った。つっぱりが詰まっていることがわかるし、ウレタンだとシャープな角が出なくて角の丸まったひし形になってしまった。ちょうどの大きさのポリスチレンつっぱりと表面のなめらかな薄紙がいいかもしれない。まあ、どっちにしても、はっきり言って安っぽい。

でも、僕の場合、計算が正しいことがわかればそれでいい。ちょっと負け惜しみくさいけど。

ちなみに今回作った型紙はここにpdfで。等倍でプリントアウトして組むと円の直径、すなわちひし形の対角線の長さが4cmになる。つっぱり用の断面は本来の大きさと、周囲を1mmだけ小さくした（-1mmと書いてある）ものを作った。これを目安に適当なぶんを削り落とせばいい。

それと、高さはこれではちょっと短いかもしれない。

還暦のジジイが暇にまかせて遊んでる、という雰囲気だけど、ほんとは僕にはこんなことして優雅に遊んでる暇はないんだ。いかんいかん。