AnglePathとAnglePath3D [日常のあれやこれや]
またMathematicaで遊ぶネタ。会社のお金でMathematicaのライセンスを手に入れたけど、最新版でないといけないということはぜんぜんしてなくて、せいぜい6.0のころの機能しか使ってない。今や知らない関数や機能の方が何倍も多くなってしまった。
僕はどうも根が貧乏性なもんで、なんとなくもったいないような気がして、ときどき思い出しては新しい機能を勉強しようとしてるんだけど、使いこなすところまでなかなかたどり着けない。で、今日たまたま見つけたMathematica6.0にはなかった関数AnglePathとAnglePath3Dが結構面白かったのでちょっと書いておく....
AnglePathは角度のリストを与えると2次元平面上で単位長さ進んでから最初の角度だけ曲がって、また単位長さ進んでは次の角度曲がって、ということをリストが尽きるまで繰り返してその座標のリストを返す。こんなの組み込み関数にしないでFoldListかなんか使って書けばいいようなもんだとも思ったけど、ついいじって遊んでしまった。
角度リストに$2\pi$を割り切る同じ値の繰り返しを与えると正多角形を描く、というのはすぐわかる。例えば
同じように、進んだ距離に比例した角度のリスト(つまり、角度を一定の単位ずつ増やしたリスト)を与えると、これはいわゆるクロソイド曲線になる。こんなやつ。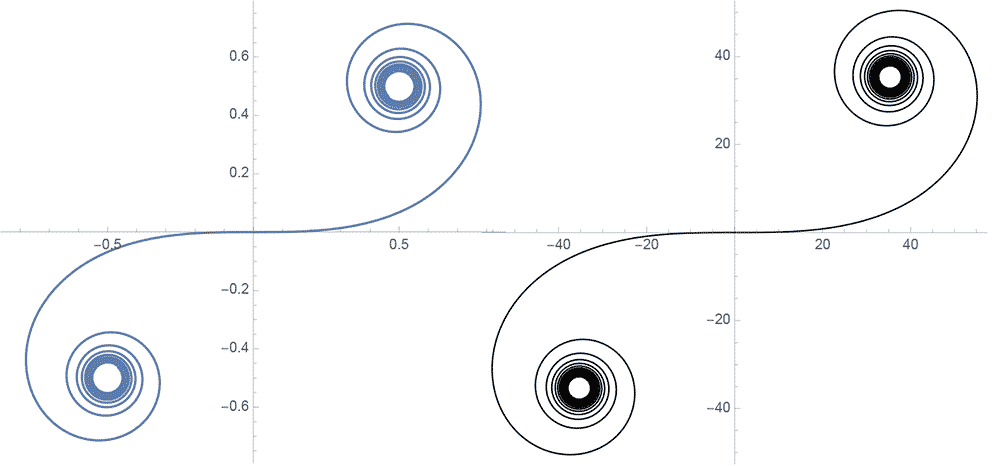 左はMathematica組み込み関数のフレネル積分FresnelCとFresnelSで描いたもので、右はAnglePathを使って描いたもの。こんなコードで
左はMathematica組み込み関数のフレネル積分FresnelCとFresnelSで描いたもので、右はAnglePathを使って描いたもの。こんなコードで
光学屋にはクロソイドというよりは「コルニュのスパイラル」と呼ぶ方が馴染みがある。一様に照明された半無限ナイフエッジのフレネル回折による場の大きさが、cos積分の方を実部にsin積分を虚部にしたものに比例する、というのは中途半端な距離の回折に悩まされた経験のある光学屋ならお馴染みである。
クロソイドやフレネル回折では曲率無限大のところへ収束してしまうけど、AnglePathでは$2\pi$を超えた値でも指定できるので、リストの角度を増やしていくと渦巻きの中心から脱出してくる。角度の刻みが$2\pi$を割り切るような値でない場合は、元のところへは戻ってこないで、他の位置に次の螺旋を描くことになる。その次の螺旋がどこに作られるかは、角度の刻みに敏感に依存する。$2\pi$の何倍も超えて螺旋が何十個何百個できるようなAnglePathの軌跡は典型的なカオスになる。
例えばこんなふうに
YouTube動画の埋め込みがやっぱりうまくいかない。iframe動かない)。
ほんのすこし(百万分の1°)変えるだけで螺旋の位置がずれていくことがわかる。したがってこんなコード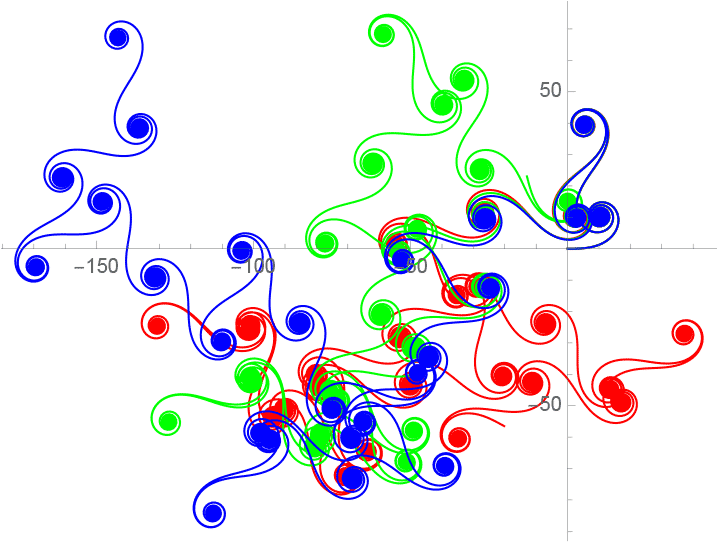 となって、3つめの螺旋まではこの絵では重なって見えるけど、そのあとは全然違ってくるというのがわかる。
となって、3つめの螺旋まではこの絵では重なって見えるけど、そのあとは全然違ってくるというのがわかる。
これだけだったら、ほー、カオスだねぇ、で終わるんだけど、MathematicaにはAnglePathの3次元版AnglePath3Dというのがある。AnglePathでは2次元だったので角度の指定はひとつだけだったけどAnglePath3Dはオイラー角で指定するようになっている。ひとつ悲しいことがあってAnglePath3Dは11.1で組み込み関数になったものらしくて、残念ながらRaspbianのMathematicaでは動かない。
これを使ってこんな
もっと長いのを描いてみる。間違い探しみたいにパラメータをちょっとだけ変えた3本の3次元コルニュ(この名前はおかしいか)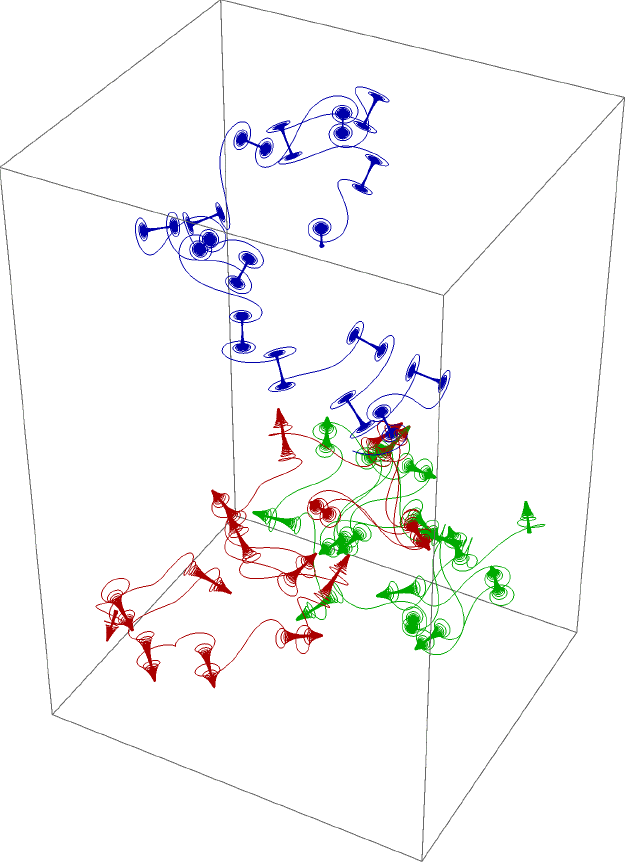 となる。なんだか小さなバネがこんがらがったみたいにみえる。ランダムウォークでも2次元と3次元では特徴が違ってくるのと同じようにAnglePath3Dだと振る舞いも違ってくる。なんだか面白い。
となる。なんだか小さなバネがこんがらがったみたいにみえる。ランダムウォークでも2次元と3次元では特徴が違ってくるのと同じようにAnglePath3Dだと振る舞いも違ってくる。なんだか面白い。
実はずっと昔、なんのためだったか忘れたんだけどなにかのシミュレーションのために、1回で大きくは曲がらない(おおよそ前を向いて歩く)ランダムウォークをMathematicaで書いた。そのときAnglePathがあったら1行で済んでいたということになる。
でもこのAnglePathってこういう遊び以外に、何に使えるんだろ?
僕はどうも根が貧乏性なもんで、なんとなくもったいないような気がして、ときどき思い出しては新しい機能を勉強しようとしてるんだけど、使いこなすところまでなかなかたどり着けない。で、今日たまたま見つけたMathematica6.0にはなかった関数AnglePathとAnglePath3Dが結構面白かったのでちょっと書いておく....
AnglePathは角度のリストを与えると2次元平面上で単位長さ進んでから最初の角度だけ曲がって、また単位長さ進んでは次の角度曲がって、ということをリストが尽きるまで繰り返してその座標のリストを返す。こんなの組み込み関数にしないでFoldListかなんか使って書けばいいようなもんだとも思ったけど、ついいじって遊んでしまった。
角度リストに$2\pi$を割り切る同じ値の繰り返しを与えると正多角形を描く、というのはすぐわかる。例えば
With[{n = 8}, Graphics[Line[AnglePath[ConstantArray[2 Pi/n, n]]]]]
は正八角形を描く。ランダムな角度のリストはランダムウォーク(酔歩)になる。同じように、進んだ距離に比例した角度のリスト(つまり、角度を一定の単位ずつ増やしたリスト)を与えると、これはいわゆるクロソイド曲線になる。こんなやつ。

Graphics[Line[AnglePath[Range[0, Pi/8, 2 Pi/10000]]]]単位長さを合わせなかったのでスケールは違ってしまったけど、形はよく似ている(このコードでは上半分しか描かない。出発の向きを180°変えることで下半分になる)。
光学屋にはクロソイドというよりは「コルニュのスパイラル」と呼ぶ方が馴染みがある。一様に照明された半無限ナイフエッジのフレネル回折による場の大きさが、cos積分の方を実部にsin積分を虚部にしたものに比例する、というのは中途半端な距離の回折に悩まされた経験のある光学屋ならお馴染みである。
クロソイドやフレネル回折では曲率無限大のところへ収束してしまうけど、AnglePathでは$2\pi$を超えた値でも指定できるので、リストの角度を増やしていくと渦巻きの中心から脱出してくる。角度の刻みが$2\pi$を割り切るような値でない場合は、元のところへは戻ってこないで、他の位置に次の螺旋を描くことになる。その次の螺旋がどこに作られるかは、角度の刻みに敏感に依存する。$2\pi$の何倍も超えて螺旋が何十個何百個できるようなAnglePathの軌跡は典型的なカオスになる。
例えばこんなふうに
ap = Table[
AnglePath[Range[0, 5 Pi, N[2/720 Pi (1 + c/100000)]]], {c, 0,
120}];
単位長さいくたびに0.5°ずつ増やしていったAnglePathで、パラメータcによって0.5°にほんのわずか(といっても機械精度実数の限界があるけど)0.000001°ずつ増やしていったときの変化を動画にして見たのがこれ(YouTubeにジャンプします。
YouTube動画の埋め込みがやっぱりうまくいかない。iframe動かない)。
ほんのすこし(百万分の1°)変えるだけで螺旋の位置がずれていくことがわかる。したがってこんなコード
With[{upto = 50 Pi, step = 2 Pi/1000 + 0.001, diff = 10^-8},
Graphics[{{Red,
Line[AnglePath[Range[0, upto, step + diff]]]}, {Green,
Line[AnglePath[Range[0, upto, step + 2 diff]]]}, {Blue,
Line[AnglePath[Range[0, upto, step + 3 diff]]]}}, Axes -> True]]
つまりちょっとずつ($10^{-8}$rad)変えて3本描いてみると

これだけだったら、ほー、カオスだねぇ、で終わるんだけど、MathematicaにはAnglePathの3次元版AnglePath3Dというのがある。AnglePathでは2次元だったので角度の指定はひとつだけだったけどAnglePath3Dはオイラー角で指定するようになっている。ひとつ悲しいことがあってAnglePath3Dは11.1で組み込み関数になったものらしくて、残念ながらRaspbianのMathematicaでは動かない。
これを使ってこんな
alphas = Range[0, 10, .001];
ap3 = Table[
AnglePath3D[{Pi/2, 0, 0},
Transpose[{alphas, ConstantArray[-0.001 c, Length[alphas]]}]], {c,
0, 100}];
つまり$z$軸周りの回転は2次元のAnglePathと同じようにして、$x$軸周りの回転をちょっとずつ増やしていく(みっつめの自由度はここでは0にしている)。$x$軸周りの回転が0なら2次元と同じになるけど、増えていくとだんだん2次元平面から離れていくはずである。上を実行してムービーにしたのがこれ(YouTubeにジャンプします)
なんか植物のツルが成長するタイムラプスでも見てるような気分になる。しかしこれ、僕が思ってたのと違う動きをする。なんで細長くなるんだろ?ピンとこない。もっと長いのを描いてみる。間違い探しみたいにパラメータをちょっとだけ変えた3本の3次元コルニュ(この名前はおかしいか)
With[{as1 = Range[0, 100, 0.0010000], as2 = Range[0, 100, 0.00100001]},
ls1 = AnglePath3D[{Pi/2, 0, 0},
Transpose[{as1, ConstantArray[0.01, Length[as1]],
ConstantArray[0.01, Length[as1]]}]];
ls2 = AnglePath3D[{Pi/2, 0, 0},
Transpose[{as2, ConstantArray[0.01, Length[as2]],
ConstantArray[0.01, Length[as2]]}]];
ls3 = AnglePath3D[{Pi/2, 0, 0},
Transpose[{as1, ConstantArray[-0.01, Length[as1]],
ConstantArray[0.001, Length[as1]]}]];
Graphics3D[{Darker[Red], Line[ls1], Darker[Green], Line[ls2],
Darker[Blue], Line[ls3]}]]
これを実行すると

実はずっと昔、なんのためだったか忘れたんだけどなにかのシミュレーションのために、1回で大きくは曲がらない(おおよそ前を向いて歩く)ランダムウォークをMathematicaで書いた。そのときAnglePathがあったら1行で済んでいたということになる。
でもこのAnglePathってこういう遊び以外に、何に使えるんだろ?
2017-05-28 21:38
nice!(0)
コメント(0)
トラックバック(0)




コメント 0