ガウシアンビームの光学 - その8 [ガウシアンビーム]
ガウシアンビームを自由空間の波動方程式から導こうと言う話の続き。その1でHelmholtzの方程式、その2で平面波の解、その3で近軸波動方程式、その4で軸対称解に方程式を変形、その5で解をガウシアンの形を仮定、その6で解を書き下して、その7では解の性質を調べる手始めとしてエネルギーを計算した。
今回は、解に入っていた積分定数が物理的にどんな意味があるかを考える...
$z_R$は長さの次元を持つ積分定数だった。物理的な意味を探るためにエネルギー密度の式(式-7:1)をもう一度思い出すと$U(r,z)$は \begin{align} U(r,z) &= u(z)g_z(r) \\ u(z) &= \frac{w_0^2}{w(z)^2} \nonumber \\ g_z(r) &= \exp \left(-2\frac{r^2}{w(z)^2} \right) \nonumber \end{align} となっていて、$g_z(r)$は$r$に関してガウス関数そのものである。さらに \begin{align} w_0 &= \sqrt{\displaystyle \frac{2z_R}{k}} \nonumber \\ w(z) &= w_0 \sqrt{ 1+(z/z_R)^2} \nonumber \end{align} だったので波長と$z_R$を決めると$w_0$は定数で、$w(z)$は$z=0$のところで最小値$w_0$になるような関数になっている。そして$g_z(r)$には肩の分母に$w(z)$が入っているのでガウシアンの幅を強度がピークの$1/e^2$に下がる半径で決めるとするとそれはすなわち$w(z)$であるということになる。
そのことから$z=0$の位置をガウシアンビームのビームウェスト(beam waist、一番細いところという意味で)と呼ぶ。そして$w_0$をウェスト半径(ガウシアンの最大強度の$1/e^2$になる位置)と呼ぶ。
ウェスト付近の$ -z_R \lt z \lt z_R $の範囲はビーム全体から見ればエネルギーが集中している付近である、ということが言えるので、$z=\pm z_R$の場合を考えてみると \begin{equation} U(r,z_R) = \frac{1}{2} \exp \Bigg( -2\frac{r^2}{ \left(\sqrt{2}w_0 \right)^2} \Bigg) \nonumber \end{equation} となる。つまり$z=\pm z_R$では$z=0$のところにくらべて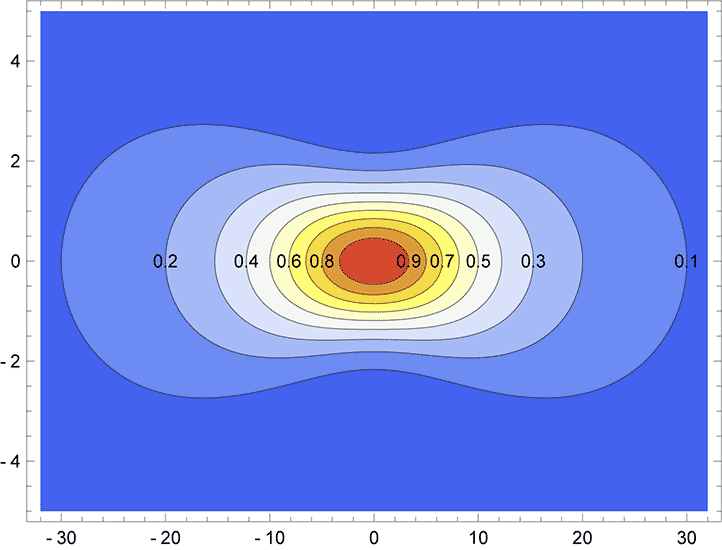 に示す。$r=0$の上では$z_R=10$mmのところで0.5の等高線が走っていることがわかる。
に示す。$r=0$の上では$z_R=10$mmのところで0.5の等高線が走っていることがわかる。
また、ガウシアンの$g_z(r)$の部分だけの等高線表示をこの図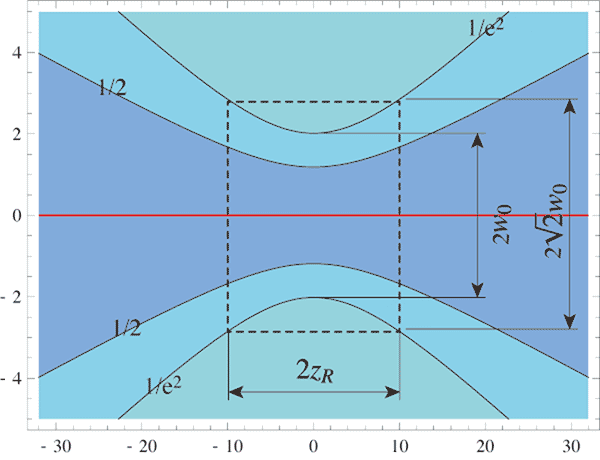 に示す。
に示す。
図中、$1/e^2$の等高線が一番狭まった部分の幅が$2w_0$で、$z=\pm z_R$の位置でその$\sqrt{2}$倍になっていることを示している。
これまでただの「積分定数」と呼んできたパラメータを、ガウシアンビームのエネルギーが一番集中した領域の大きさを表す値であると見なして、この長さ$z_R$をRayleigh長さ、$z=\pm z_R$の領域をRayleigh領域(あるいはRayleighレンジ)と呼ぶ。
何度も式を書いたように、ビームウェスト自身も当然$z_R$に依存していて、さらにもう一度いくつかの書き方をしてみると \begin{align} w_0 &= \sqrt{\displaystyle \frac{2z_R}{k}} \nonumber \\ &=\sqrt{\frac{\lambda z_R}{\pi}} \nonumber \\ z_R &= \frac{k w_0^2}{2} \nonumber \\ &= \frac{\pi w_0^2}{\lambda} \nonumber \end{align} などと書ける。つまりビームウェストは$z_R$が小さいと小さくなる。言い換えればRayleigh領域が小さいほどビームは細い、ということになる。では、いくらでもビームは細くできるのか、というのはこのあとすぐ考える。
今回は、解に入っていた積分定数が物理的にどんな意味があるかを考える...
3.2 パラメータ$z_R$の物理的な意味
ガウシアンビームにはパラメータがひとつだけあった。それがなにかを考えてみる。$z_R$は長さの次元を持つ積分定数だった。物理的な意味を探るためにエネルギー密度の式(式-7:1)をもう一度思い出すと$U(r,z)$は \begin{align} U(r,z) &= u(z)g_z(r) \\ u(z) &= \frac{w_0^2}{w(z)^2} \nonumber \\ g_z(r) &= \exp \left(-2\frac{r^2}{w(z)^2} \right) \nonumber \end{align} となっていて、$g_z(r)$は$r$に関してガウス関数そのものである。さらに \begin{align} w_0 &= \sqrt{\displaystyle \frac{2z_R}{k}} \nonumber \\ w(z) &= w_0 \sqrt{ 1+(z/z_R)^2} \nonumber \end{align} だったので波長と$z_R$を決めると$w_0$は定数で、$w(z)$は$z=0$のところで最小値$w_0$になるような関数になっている。そして$g_z(r)$には肩の分母に$w(z)$が入っているのでガウシアンの幅を強度がピークの$1/e^2$に下がる半径で決めるとするとそれはすなわち$w(z)$であるということになる。
そのことから$z=0$の位置をガウシアンビームのビームウェスト(beam waist、一番細いところという意味で)と呼ぶ。そして$w_0$をウェスト半径(ガウシアンの最大強度の$1/e^2$になる位置)と呼ぶ。
ウェスト付近の$ -z_R \lt z \lt z_R $の範囲はビーム全体から見ればエネルギーが集中している付近である、ということが言えるので、$z=\pm z_R$の場合を考えてみると \begin{equation} U(r,z_R) = \frac{1}{2} \exp \Bigg( -2\frac{r^2}{ \left(\sqrt{2}w_0 \right)^2} \Bigg) \nonumber \end{equation} となる。つまり$z=\pm z_R$では$z=0$のところにくらべて
- ガウシアンのピーク強度は半分に下がる
- ガウシアンの幅は$\sqrt{2}$倍に広がる

また、ガウシアンの$g_z(r)$の部分だけの等高線表示をこの図

図中、$1/e^2$の等高線が一番狭まった部分の幅が$2w_0$で、$z=\pm z_R$の位置でその$\sqrt{2}$倍になっていることを示している。
これまでただの「積分定数」と呼んできたパラメータを、ガウシアンビームのエネルギーが一番集中した領域の大きさを表す値であると見なして、この長さ$z_R$をRayleigh長さ、$z=\pm z_R$の領域をRayleigh領域(あるいはRayleighレンジ)と呼ぶ。
何度も式を書いたように、ビームウェスト自身も当然$z_R$に依存していて、さらにもう一度いくつかの書き方をしてみると \begin{align} w_0 &= \sqrt{\displaystyle \frac{2z_R}{k}} \nonumber \\ &=\sqrt{\frac{\lambda z_R}{\pi}} \nonumber \\ z_R &= \frac{k w_0^2}{2} \nonumber \\ &= \frac{\pi w_0^2}{\lambda} \nonumber \end{align} などと書ける。つまりビームウェストは$z_R$が小さいと小さくなる。言い換えればRayleigh領域が小さいほどビームは細い、ということになる。では、いくらでもビームは細くできるのか、というのはこのあとすぐ考える。
2017-06-01 21:50
nice!(0)
コメント(0)
トラックバック(0)


コメント 0