円錐の交差

川合工房さんにコメントを頂いたので久しぶりにペーパークラフトネタ。僕には川合工房さんのような造形やテクスチャの美しさに対するセンスはないので、僕にもできるアプローチにする。

問題の答えはちょっと遠慮して、回答が出たら一般論を書いてみることにする。今日は円錐の折り返しについて。

扇形を一度折って円錐台にすると、ぺらぺらだった紙が強度を増す。これにドーナッツ形の底を糊で貼れば剛体になる。紙は曲がるけど伸び縮みは少なく、紙の一方の面の曲げ方向がもう一方の伸び縮み方向になるように組み合わせれば強度が増える。これはペーパークラフトだけでなく軽くて固いものを作るときの基本だけど、ペーパークラフトで大きな作品を作るときにも考慮すればぐにゃぐにゃしないものにできる。円錐台の組み合わせはペーパークラフトの強度を保つ上で基本的な要素。

上下逆を向いた二つの円錐台が交差する形は、円錐の軸が一致している場合川合工房さんのように折るだけで実現できて切り貼りのない美しい面にすることができる。ペーパークラフトは「切る」「貼る」だけでなく適切な場所に「曲げる」「折る」が含まれることが造形の上では重要な要素である。

たとえばさっきの円錐台の交差は円錐の軸が一致してるときには折ることで実現できるけど、軸が一致していない場合はどうなるのか、というとそれぞれに軸が平行な場合であっても完全に一致していなければ「折る」だけでは実現できないことが数学的に証明できる。ペーパークラフトで「できない」ことを証明しても何の意味もないので面白いことができないか考えてみる。

具体的に言えば川合工房さんの円錐台はこんな上下を向いたふたつの円錐の重ねあわせの一部であることがわかる。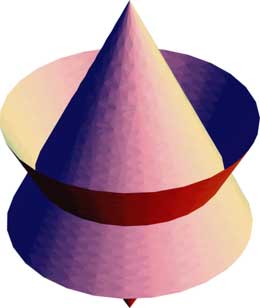

これはふたつの円錐の軸は一致している。実際に紙を折って作ってみるとこんなふうになる。あまりきれいじゃないけど。

ではこんなのは可能なのか？

これは、軸は平行だけど横にずれている。実はこれはさっきも書いたけど折るだけでは実現できない。しかし、対称性はあるので同心円に折る前に、まず扇形をある曲線に沿ってこんなふうにふたつに切り離す。

そしてそれぞれを円錐（の一部）になるように丸めて一方を軸のまわりに180°回転させる。そうするとあら不思議、ぴったりとおさまって平行にずれた円錐の交線で折れ返った形ができる。

川合工房さんの記事にある角度χ°はこの図形でもぐるっと全部同じになる。

この立体の型紙をここに置いておく。2ページのpdfファイルになっていて1ページ目は軸が一致している場合とずれている場合の展開図になっている。2ページ目は軸がずれているときののりしろ付きの展開図。実際に作るときはこっちの方がいい。みっつあるAのかどとBのかどがそれぞれ一致するように組み立てればいい。山吹色ののりしろ部分は縦に切れ目を入れて曲線に沿うようにする。

これは空間図形の対称性のおかげ。このふたつの円錐の交線（この立体の尾根線）は空間のなかで、ある平面内の楕円になっている。

円錐の式をふたつ連立させて解けばその空間曲線は求まる。そこまでは簡単。ではここで僕からの問題。

軸が一致した円錐に組み立てられる折り線は展開図では円錐の外形線と同じ円弧になるが、もう一方の軸のずれた円錐に組み立てられるように、展開図の扇形を切る曲線は2次元平面上のどんな式で表されるか？

媒介変数表示で上手く変数を選べば比較的簡単な有理関数になる。正解者には豪華景品を進呈します。いや、すみません、何も出ません。

コメント 2

楽しい出題ありがとうございます。楕円でしょう、と決めつけて折ってみたら変なものが出来ました。正解ではないにしても、これは一体何だろう？　正解の方はさらに紙をひねって考えてみます。
　ところでdecafish様も正解として景品を進呈しますので、よろしければこちらまでメイルをくださいませ。 　[e-mail]

by 川合工房 (2010-02-17 23:10) 

コメントありがとうございます。
立体としての空間曲線は楕円になります。平面に展開するとそれが歪んだ曲線になります。でもこの場合は楕円関数のような変な式ではなくて比較的簡単な式になります。川合工房さんの問題の解答を含めて改めて整理したいと思います。
ところで川合工房さんの景品が僕も欲しいのであとでメールします。よろしくお願いします。
by decafish (2010-02-18 21:12)