近軸光線追跡 - その2 [近軸光線追跡]
昨日から近軸追跡のメモを始めた。それほど難しくないけど、厳密なことを言わなければ他への参照はMaxwellの方程式だけにしたい。そのために論旨にはそれなりに悩むが、個人のメモとしてはあまり意味のない悩みではある。
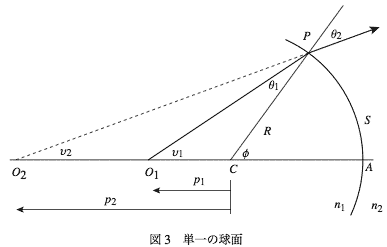 光線がO1から出発して、それぞれ屈折率n1とn2を持つ媒質が接している境界面Sの点Pに入射するところを考える。面Sは球面であるとする。点Pで光は屈折する。Pでの入射角をθ1、屈折角をθ2とする。
光線がO1から出発して、それぞれ屈折率n1とn2を持つ媒質が接している境界面Sの点Pに入射するところを考える。面Sは球面であるとする。点Pで光は屈折する。Pでの入射角をθ1、屈折角をθ2とする。
このとき である。点O1と境界面の中心Cを延長してSと交わる点をAとする。O1、C、A、Pそして屈折光線はすべてひとつの平面の上に乗る。直線OCを前後に延長した直線をここでは光軸と呼ぶことにする。
である。点O1と境界面の中心Cを延長してSと交わる点をAとする。O1、C、A、Pそして屈折光線はすべてひとつの平面の上に乗る。直線OCを前後に延長した直線をここでは光軸と呼ぶことにする。
屈折光線を延長して光軸と交わる点をO2とする。図-3では左側で交わっているが、場合によっては右側になることもある。
図のように光軸と光線のなす角度をυ1、υ2とする。また光軸と直線CPのなす角度をϕとする。
当然 である。ただし、直線CO1の長さをp1、CO2の長さをp2とした。
である。ただし、直線CO1の長さをp1、CO2の長さをp2とした。
ところでこういう場合、符号を決めておくと便利である。ここでは面から右側に距離をはかるときに正、角度は光軸から反時計回りにはかるときに正とする。
例えば図-3のp1、p2の距離は負、υ1やυ2、ϕなどの角度は正である。そうするとθ1などは正でなければならない、ということになる。
三角関数の正弦定理から なのでSnellの法則から
なのでSnellの法則から
 と書ける。これはひとつの光線にふたつの変数piとυiを含んだ式になっているが、その交点の位置Pは共通なのでもうひとつの式、例えば
と書ける。これはひとつの光線にふたつの変数piとυiを含んだ式になっているが、その交点の位置Pは共通なのでもうひとつの式、例えば
 などというような式が連立している、とみなす必要がある(点Pで光線が交わるとしてpi、υiの関係を解くとこうなる)。これを解くのは非常に煩わしい。ベクトル表現などした方がまだましだけど、面倒なことに変わりはない。
などというような式が連立している、とみなす必要がある(点Pで光線が交わるとしてpi、υiの関係を解くとこうなる)。これを解くのは非常に煩わしい。ベクトル表現などした方がまだましだけど、面倒なことに変わりはない。
ここで光軸からの角度が小さいとして と展開して1次までとると式-13は
と展開して1次までとると式-13は
 となるが、s1 = p1 + Rなどとして
となるが、s1 = p1 + Rなどとして
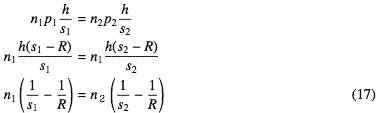 と書ける。ここでhはPの光軸からの高さでtani ≈ siniとした。この関係をAbbeの普遍式という。
と書ける。ここでhはPの光軸からの高さでtani ≈ siniとした。この関係をAbbeの普遍式という。
こういう角度に関して1次までとる近似を近軸近似あるいはGauss近似と呼ぶ。またこれが成立するとみなせる範囲を近軸領域、あるいはGauss領域などと呼ぶ。
式-17は角度によらない式になったのでs1が決まるとs2も決まってしまう、つまりO1から出た光はPの位置によらずO2を通る(図-3のように後ろ向きの場合もある)ことになる。このO1とO2の関係を共役(Conjugate)と言う。くどいようだが、この共役という関係は近軸の概念である。Abbeの普遍式は面を隔てた領域間で共役をあらわす基本的な式である。
しかし、もとの厳密な式-13は、もちろんPの位置によってp2の長さ、つまりO2の位置は変化する。これはさっきの平面での屈折でも見た現象である。平面の場合は屈折する位置によらなくなる位置は無限遠の場合だけだった。この場合はどうか。
3.2 境界が球面状の場合
図-3のように境界面が球面(の一部)の場合を考える。
このとき
屈折光線を延長して光軸と交わる点をO2とする。図-3では左側で交わっているが、場合によっては右側になることもある。
図のように光軸と光線のなす角度をυ1、υ2とする。また光軸と直線CPのなす角度をϕとする。
当然
ところでこういう場合、符号を決めておくと便利である。ここでは面から右側に距離をはかるときに正、角度は光軸から反時計回りにはかるときに正とする。
例えば図-3のp1、p2の距離は負、υ1やυ2、ϕなどの角度は正である。そうするとθ1などは正でなければならない、ということになる。
三角関数の正弦定理から


ここで光軸からの角度が小さいとして

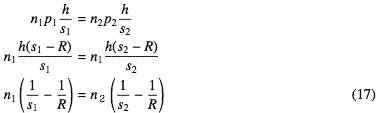
こういう角度に関して1次までとる近似を近軸近似あるいはGauss近似と呼ぶ。またこれが成立するとみなせる範囲を近軸領域、あるいはGauss領域などと呼ぶ。
式-17は角度によらない式になったのでs1が決まるとs2も決まってしまう、つまりO1から出た光はPの位置によらずO2を通る(図-3のように後ろ向きの場合もある)ことになる。このO1とO2の関係を共役(Conjugate)と言う。くどいようだが、この共役という関係は近軸の概念である。Abbeの普遍式は面を隔てた領域間で共役をあらわす基本的な式である。
しかし、もとの厳密な式-13は、もちろんPの位置によってp2の長さ、つまりO2の位置は変化する。これはさっきの平面での屈折でも見た現象である。平面の場合は屈折する位置によらなくなる位置は無限遠の場合だけだった。この場合はどうか。
2010-09-22 22:22
nice!(0)
コメント(0)
トラックバック(0)


コメント 0