楽譜アーカイブアプリ - その24 Lanczos関数のBicubic化 [考え中の問題]
今日は先日までの脱線の締めくくり。もうちょっとで忘れるところ。継続とは自分の記憶力との戦いである、なんていうのは僕だけか。
ところが画像回転のようなアプリケーションではチャンネルあたり8ビットが一般的なので誤差が0.4%以下になれば実質的に区別がつかない。そこでLanczos関数も定義式通りに計算するのではなく、さっきと同じやり方でLanczos関数を3次のスプライン関数で置き換えれば、数値評価のオーバーヘッドを減らすことができる。さらに数値的ににも安定な関数にすることができる。
そのためにはLanczos関数の微係数を計算すればいい。積の微分から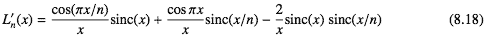 となる。あってるよな。xが整数での値は整理すると、kを整数として
となる。あってるよな。xが整数での値は整理すると、kを整数として
 となる。あってるよな。この式だとx=0では確定しないけどちゃんともとの連続な式の極限は0になる。他の点でもこれはもとのsinc関数のように簡単な値にはならない。
となる。あってるよな。この式だとx=0では確定しないけどちゃんともとの連続な式の極限は0になる。他の点でもこれはもとのsinc関数のように簡単な値にはならない。
具体的な形を書いてみると
まず区間[0,1]では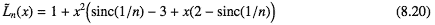 1 ≤ k < n−1の区間[k,k+1]では
1 ≤ k < n−1の区間[k,k+1]では
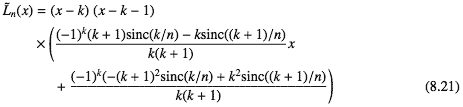 さいごの区間[n−1,n]では
さいごの区間[n−1,n]では
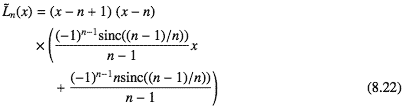 となる。式はうるさいけど、面倒な係数はみんな整数の式なので数値評価してしまえばいい、すなわちnを決め打ちしてしまうと数値が確定するのでその値を使えばいい。
となる。式はうるさいけど、面倒な係数はみんな整数の式なので数値評価してしまえばいい、すなわちnを決め打ちしてしまうと数値が確定するのでその値を使えばいい。
これで5次までのLanczos関数を作って本来のLanczos関数との差分をプロットしてみたのkが図-8.4である。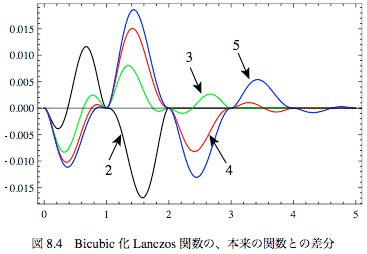 もとのLanczos関数との誤差はピークの値の2%以下の範囲に収まることになる。目標の0.4%よりはかなり大きいけれど、画像の補間などの用途には実質的に十分だろう。これを使えば計算コストは当然Bicubic拡張と同じになる。もちろんsinc関数のx=0付近の数値不安定性はこの関数だと現れないので使いやすい。
もとのLanczos関数との誤差はピークの値の2%以下の範囲に収まることになる。目標の0.4%よりはかなり大きいけれど、画像の補間などの用途には実質的に十分だろう。これを使えば計算コストは当然Bicubic拡張と同じになる。もちろんsinc関数のx=0付近の数値不安定性はこの関数だと現れないので使いやすい。
2%の誤差が気に入らないなら、5次のスプライン関数にして2回微分まで考慮すればいい。あるいはチェビシェフ近似を使えば誤差のピーク値は押さえ込むことができる。しかしそこまでする必要があるか、という気はする。僕はやらないので本来のLanczos関数での結果と1ビットもずれてはならない、と考えている人はやって欲しい。
こういうのってたぶんすでに誰かやってるはずだとは思うんだけど、僕は見つけられなかった。もし他にないなら、これはメリットあるので式の係数を書き出しておく。
一応チェックした。間違ってないと思う。係数が正負かわりばんこにでてくるのも、いかにも「ベキで展開しました」と言う感じがあって、もっともらしいし。
 である。ただしnはLanczosの次数(考慮する格子点の距離)で、Nは次元数(2次元画像の場合には2)である。また、足し算回数も同じになる。一般のライブラリにあるsinc関数を使った場合に較べれば精度を犠牲にした分、数倍効率がいいはずである。
である。ただしnはLanczosの次数(考慮する格子点の距離)で、Nは次元数(2次元画像の場合には2)である。また、足し算回数も同じになる。一般のライブラリにあるsinc関数を使った場合に較べれば精度を犠牲にした分、数倍効率がいいはずである。
デメリットとしては
もとのLanczos関数と画像補間の比較をした方がいいけど、めんどうなのでここではやらない。実装のときにその気があればやってみよう。
8.1.6 Lanczos関数のBicubic化
普通sinc関数の数値評価は結構複雑なことをする。例えばgslの場合- 引数が0.8以下だったらチェビシェフ展開された関数を使う
- 100.0以下だったら定義式通りの計算を行う
- それ以上だったら定義式に従って計算して誤差評価を厳密に行う作業を追加する
ところが画像回転のようなアプリケーションではチャンネルあたり8ビットが一般的なので誤差が0.4%以下になれば実質的に区別がつかない。そこでLanczos関数も定義式通りに計算するのではなく、さっきと同じやり方でLanczos関数を3次のスプライン関数で置き換えれば、数値評価のオーバーヘッドを減らすことができる。さらに数値的ににも安定な関数にすることができる。
そのためにはLanczos関数の微係数を計算すればいい。積の微分から
具体的な形を書いてみると
まず区間[0,1]では
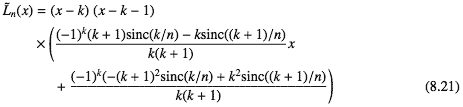
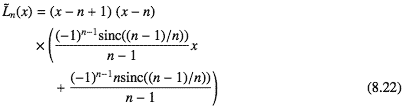
これで5次までのLanczos関数を作って本来のLanczos関数との差分をプロットしてみたのkが図-8.4である。

2%の誤差が気に入らないなら、5次のスプライン関数にして2回微分まで考慮すればいい。あるいはチェビシェフ近似を使えば誤差のピーク値は押さえ込むことができる。しかしそこまでする必要があるか、という気はする。僕はやらないので本来のLanczos関数での結果と1ビットもずれてはならない、と考えている人はやって欲しい。
こういうのってたぶんすでに誰かやってるはずだとは思うんだけど、僕は見つけられなかった。もし他にないなら、これはメリットあるので式の係数を書き出しておく。
8.1.7 Bicubic近似Lanczos2関数の係数
| 定義域 | x3 | x2 | x | 1 |
| 0 ≤ x < 1 | 1.36338 | -2.36338 | 0 | 1 |
| 1 ≤ x < 2 | -0.63662 | 3.1831 | -5.09296 | 2.54648 |
| 2 ≤ x | 0 | 0 | 0 | 0 |
8.1.8 Bicubic近似Lanczos3関数の係数
| 定義域 | x3 | x2 | x | 1 |
| 0 ≤ x < 1 | 1.17301 | -2.17301 | 0 | 1 |
| 1 ≤ x < 2 | -0.620245 | 3.30797 | -5.58221 | 2.89448 |
| 2 ≤ x < 3 | 0.206748 | -1.65399 | 4.34172 | -3.72147 |
| 3 ≤ x | 0 | 0 | 0 | 0 |
8.1.9 Bicubic近似Lanczos4関数の係数
| 定義域 | x3 | x2 | x | 1 |
| 0 ≤ x < 1 | 1.09968 | -2.09968 | 0 | 1 |
| 1 ≤ x < 2 | -0.582006 | 3.22834 | -5.61098 | 2.96465 |
| 2 ≤ x < 3 | 0.218275 | -1.84623 | 5.08395 | -4.52916 |
| 3 ≤ x < 4 | -0.100035 | 1.10039 | -4.00141 | 4.80169 |
| 4 ≤ x | 0 | 0 | 0 | 0 |
8.1.10 Bicubic近似Lanczos5関数の係数
| 定義域 | x3 | x2 | x | 1 |
| 0 ≤ x < 1 | 1.06451 | -2.06451 | 0 | 1 |
| 1 ≤ x < 2 | -0.557076 | 3.16379 | -5.59185 | 2.98513 |
| 2 ≤ x < 3 | 0.21023 | -1.85002 | 5.25574 | -4.79324 |
| 3 ≤ x < 4 | -0.109716 | 1.26534 | -4.7979 | 5.96797 |
| 4 ≤ x < 5 | 0.0584681 | -0.818553 | 3.80043 | -5.84681 |
| 5 ≤ x | 0 | 0 | 0 | 0 |
8.1.11 まとめ
この関数のメリットをもう一度まとめておくと- sinc関数の数値評価に伴う不安定性がない
- 計算コストが拡張Bicubic近似と同じで、厳密なsinc関数を使うより速い
デメリットとしては
- 厳密にはLanczos関数とは一致しない
- 2回微分以上は連続ではない
もとのLanczos関数と画像補間の比較をした方がいいけど、めんどうなのでここではやらない。実装のときにその気があればやってみよう。
2011-01-25 22:18
nice!(0)
コメント(0)
トラックバック(0)


コメント 0