厳密な光線追跡 - その10 [光線追跡エンジンを作る]
だらだらといろいろなことを書いてきたので、光線追跡の数学のツボとなる式をもう一度まとめておく。
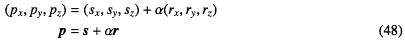 と書く。
と書く。
ここでαは媒介変数で、方向を表すベクトルrは特殊な規格化 がされているとする。ただしここでnは光線が存在する媒質の屈折率である。
がされているとする。ただしここでnは光線が存在する媒質の屈折率である。
また面も同じようにふたつの媒介変数を使って張られた点の集合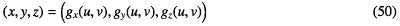 と表現する。
と表現する。
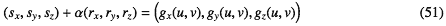 をu、v、αについて解けばよい。
をu、v、αについて解けばよい。
計算時にはとうぜん3元の連立方程式としてではなく、まずαを求めてそれを式-48に代入するほうが、無駄な計算をするのを避けられる場合がある。
その解に関して
また、簡単な場合に対して解を解析的に求めておけば、実行効率はあがるので、以下に解析解が得られる典型的な場合を列挙する。 とすると、式-<48と連立させることで
とすると、式-<48と連立させることで
 が得られる。
が得られる。
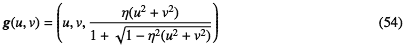 と書いた場合、平面と同じように
と書いた場合、平面と同じように
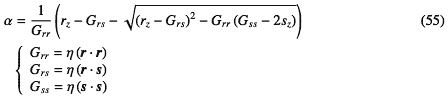 が得られる。
が得られる。
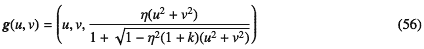 と書いた場合、
と書いた場合、
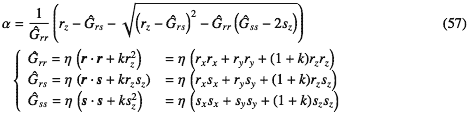 が得られる。
が得られる。
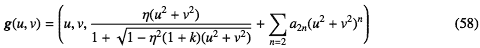 と書く。この場合は収束計算が必要になる。収束計算の初期値として第1項は2次曲面なので前節の結果を流用すればいい。
と書く。この場合は収束計算が必要になる。収束計算の初期値として第1項は2次曲面なので前節の結果を流用すればいい。
続きは次回。あとは屈折の式(Snellの法則)と座標変換について。
3.5 数学のまとめ
3.5.1 手順
光線追跡は、与えられた光線に対して- 光線と面とが交差する位置を求める
- その点での面の法線の向きから屈折角を求める
- 屈折後の光線を生成する
- 以上を、残る面に対して追跡できなくなるか、像面に到達するまで続ける
ここでαは媒介変数で、方向を表すベクトルrは特殊な規格化
また面も同じようにふたつの媒介変数を使って張られた点の集合
3.5.2 光線と面とが交差する位置
光線と面との交点は式-4と式-32とを連立させることで得られる。つまり計算時にはとうぜん3元の連立方程式としてではなく、まずαを求めてそれを式-48に代入するほうが、無駄な計算をするのを避けられる場合がある。
その解に関して
- 実数解か
- α > 0であるか
- 交点が面の定義域(クリアアパチャ)の内部か
また、簡単な場合に対して解を解析的に求めておけば、実行効率はあがるので、以下に解析解が得られる典型的な場合を列挙する。
3.5.3 平面の場合
平面の式を3.5.4 球面の場合
球面の式を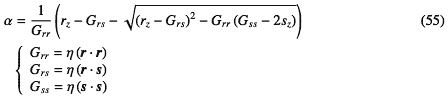
3.5.5 2次曲面の場合
2次曲面も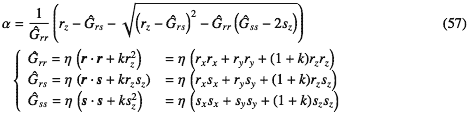
3.5.6 非球面の場合
非球面式は3.5.7 一般の面の場合
面固有の解法を与える必要がある。多くは非球面と同じ収束計算が必要になる。その場合初期値をどう選ぶかは問題で、やはり面固有のアプローチが必要になる。続きは次回。あとは屈折の式(Snellの法則)と座標変換について。
2012-10-17 21:24
nice!(0)
コメント(0)
トラックバック(0)


コメント 0