ガウシアンビームの光学 - その20

ガウシアンビームのお話の続き。これまで「その1」から「その15」まででガウシアンビームの教科書的なあつかいを（ちんたらと）まとめた。そのあと光学に固有の問題のために代表的な数値の確認、近軸理論をおさらいして、瞳から出たガウシアンビームがウェストを迎える様子、$z$、　$z_R$とは別のパラメータを考えた。今日はパラメータの取り方を含めて、ウェスト以外のところでのガウシアンビームの場を特定することを考える．．．．

6.3  中途半端な面でのガウシアンビームのパラメータ

これまで、$z_p$の位置を瞳だとしてきたけど、これはウェストから$z_p$だけ離れた任意の$x-y$平面でのビームの状態だと思ってかまわない。解を導いた径緯からこれまでガウシアンビームのパラメータとして$z_R$と$z$を使ってきた。数学的にはわかりやすいけど、前節前々節でやったように式はそれほどすっきりしないのでためしにちょっと違った値をパラメータに使ってみる。

次の図の$A$のような中途半端な位置での状態を特定することを考える。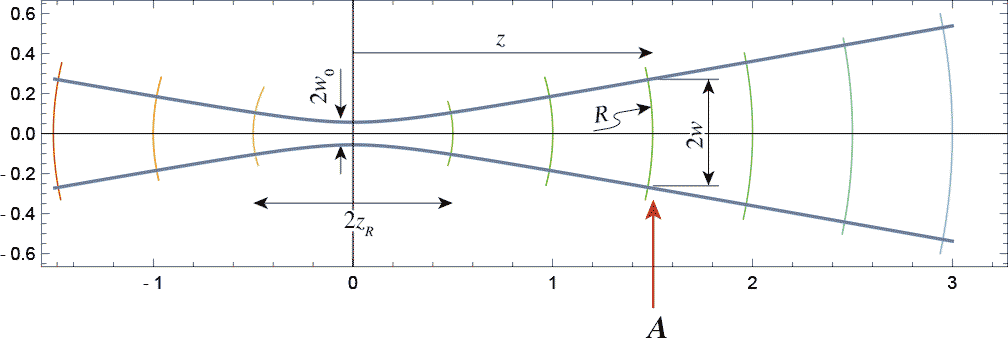

波長が決まったガウシアンビームは$z_R$を特定すれば一つに決まる。そしてウェストからの距離$z$を決めればその位置での場の状態、すなわち位相も含めた振幅分布$A(x,y)$は決まってしまう。ようするに$A$の場を特定する自由度はふたつなので、独立な変数をふたつ選んでくればいい、ということである。

そういう中途半端な位置に注目したいときには$z_R$と$z$以外に、式19:1の$\chi(z)$と式19:2の$w(z)$を使うこともできる。

$\chi$は波面の曲率なので、0では$w$はウェストになり、そのときは$z=0$で$z_R=\pi w^2/\lambda$というウェストの式になるが、0以外では$w$はウェストではなくて、どこか違ったところに$w$よりも細いウェストがある、ということで$z$の代わりになるということである。

つまり式19:1と式19:2が$z_R$や$z$による式ではなく、ある光軸に垂直な平面でのビーム波面の曲率$\chi$とビーム半径$w$のほうを独立なパラメータとすることも可能である、ということである。

$\chi$と$w$を独立なパラメータとしたとき$z$、$z_R$は解き直せばいいだけなので \begin{align} z &= \frac{\pi^2 \chi w^4}{\lambda^2+(\pi \chi w^2)^2} \label{zbychiandw} \\ z_R &= \frac{\pi \lambda w^2}{\lambda^2+(\pi \chi w^2)^2} \end{align} となって、そのときのウェスト$w_0$は \begin{equation} w_0 = \frac{\lambda w}{\sqrt{\lambda^2+(\pi \chi w^2)^2}} \end{equation} となる。

また、ついでに具体的な問題を考えると$A$の位置でのビーム半径でウェストを$z_0$の位置に作ろうとするとき、$\chi$をいくらにすればいいか、というのも知っておきたい。それは式-\ref{zbychiandw}を$\chi$について解きなおせばいいだけなので \begin{equation} \chi = \frac{1}{2z_0} \pm \sqrt{\frac{1}{4 z_0^2} - \left(\frac{\lambda}{\pi w^2}\right)^2} \end{equation} となる。あってるよな。

ビーム半径とウェストまでの位置を指定したら波面の曲率がふたつありえる、というのはちょっと前にやったウェストまでの距離を指定するとウェスト半径がふたつ出てきたのと同じ理由からである。ひとつはRayleigh領域内で、もうひとつは外に対応しているはずである、ということは計算しないでもわかる。

これまでの一連の計算でやってきたように、この下の図のように式変形に関する技術としてはガウシアンビームの計算では$z_R$（あるいは$w_0$）を含んだ式と$R(z)$（あるいは$\chi(z)$）と$w(z)$を含んだ式とを相互に入れ替えられるようにしておいたほうがいい。片方では式がぐちゃぐちゃになるけど、もう一方では簡単になる、ということがよくある。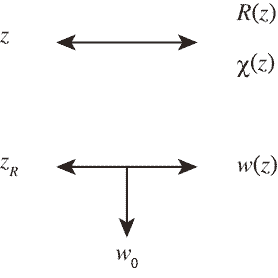

わざわざ絵にするほどのこともなかったな。この事実をこのすぐあとで使うことにする。

なぜわざわざこんなめんどくさいことを考えるかというと、ガウシアンビームのアプリケーションではレンズを使ってビームを広げたり集光したりということをする。そしてレンズはそれ自身がウェストにあるということはあまりないので、レンズの面はたいていこういう中途半端な位置にある、ということになる。