ガウシアンビームの光学 - その25 [ガウシアンビーム]
ガウシアンビームの続き。「その1」から「その15」までに教科書的な話、そのあと代表的な数値の確認、近軸理論、瞳から出たガウシアンビームがウェストを迎える様子、$z$、 $z_R$とは別のパラメータ、ガウシアンビームの場の特定法、近軸マトリクスのおさらい、近軸理論との齟齬、近軸マトリクスによるガウシアンビームの伝播計算とその個人的な印象とやってきた。今日は収差の乗ったガウシアンビームの計算法について....
ところで、ガウシアンビームの伝播計算を「そんな理想的な計算をしても意味がない」とバカにする人がいる(はっきり言えば前の会社ではそういう意見がメジャーだった)。しかし結像系レンズと違ってN.A.は低いし画角をとることはないので、理想的な計算をしても現実とよく合う、というのが僕の印象である。「全然合わない」という人は磨きのヘボなレンズを使ってるか、アラインメントがヘボなことが多い、と僕は思う。
ずっと昔(十数年前)、大阪郊外のある大学の研究施設を借りて大型定盤の上にレーザのビームを回していたある超有名電気メーカの研究者がいた。ぐるぐると飛ばしてたあげく、必要な場所に絞り込んだスポットの強度分布がぐちゃぐちゃになってて、
「こんなんあかんわ」
と言ってた。彼がほったらかしにしたので僕がそれをじっくり見ると(「続きをやる」と言ってくるかもしれないので、とりあえずいじらないでくれ、と施設の持ち主である先生から言われた。僕はそのレーザの波長で実験できればよかったので、ミラーで取り分けて巨大定盤の隅っこに配置した光学系に取り込んだ)、レーザの出口が定盤から76mmちょっと(この数字でなんのレーザを使っていたかわかるな)を合わせ鏡のクランクで150mmにしてある。そのあと結構しっかりしたスタンドに差し込んだロッドの上にレンズが固定されてて、そういうレンズをいくつか通過するうちに、定盤からの光軸の高さがいつのまにか200mmを超えていて、ロッドの長さギリギリになっている。
「あかんのはあんたのアラインメントやろ」
と密かに思っていたけど、件の人物は装置を投げ出して他所で全然別のことをやり始めた。僕はそのあとのレーザを含めた巨大定盤とそれが設置されているフロアからレンズやメカ部品をそのまま借用できることになった(そのせつは中百舌鳥の先生ありがとうございました)。当時の僕にとっては非常にありがたかったけど、これを読んだ若い光学関係者には、このエピソードから反面教師の存在を学んでいただきたい....
瞳での場は \begin{align} E(x,y) &\equiv A(x,y) \phi(x,y) \nonumber \\ &= A(x,y) \exp 2 \pi i \frac{\tau(x,y)}{\lambda} \end{align} と書ける。ここで$A$は場の大きさで、$\tau$は光路差、すなわち波面収差で、どちらも実の量である。$A$をガウシアンの電場の大きさで$\tau$に収差を仮定してFourier変換すればウェストでの場がわかって、その絶対値の2乗をとれば強度がわかる、というわけである。
しかしこれは一般の収差に関して解析的に計算できないので数値計算する必要がある。
$\rho_\delta(x,y)$の具体的な形を計算するために次の図のような、$W$と$W_\delta$の二つの波面を考える。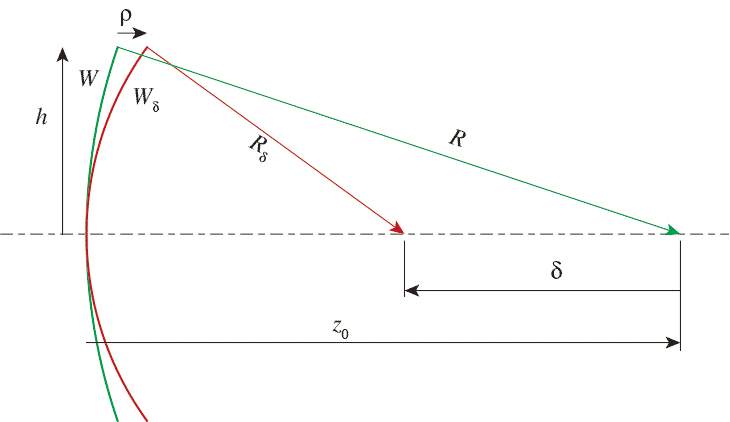 $W$は瞳から焦点位置まで$z_0$の無収差の波面とする。波面は焦点位置を中心とする球面になる。球面の半径を$R$とすると
\begin{equation}
R=z_0 \nonumber
\end{equation}
である。
焦点位置が$\delta \;(\ll z_0)$だけずれたもう一つの波面$W_\delta$を考える。図では手前に移動しているので、光学の符号の慣例によって$\delta <0$である。この波面の半径を$R_\delta$とする。
$W$は瞳から焦点位置まで$z_0$の無収差の波面とする。波面は焦点位置を中心とする球面になる。球面の半径を$R$とすると
\begin{equation}
R=z_0 \nonumber
\end{equation}
である。
焦点位置が$\delta \;(\ll z_0)$だけずれたもう一つの波面$W_\delta$を考える。図では手前に移動しているので、光学の符号の慣例によって$\delta <0$である。この波面の半径を$R_\delta$とする。
ある光軸高さ$h \;(\ll R)$での二つの波面の光路差を$\rho$とする。$\rho$が$\delta$でどう表されるかを考える。これは純粋に幾何学の問題なのでまず、 \begin{equation} \rho = \left(R_\delta-\sqrt{R_\delta^2-h^2}\right)-\left(R-\sqrt{R^2-h^2}\right) \end{equation} で、$R_\delta = R+\delta$で$R=z_0$だから \begin{equation} \rho = \left((z_0+\delta)-\sqrt{(z_0+\delta)^2-h^2}\right)-\left(z_0-\sqrt{z_0^2-h^2}\right) \end{equation} となる。これで求まったわけだけど、Fraunhofer回折領域であって、$h \ll z_0$かつ$\delta \ll z_0$としたので$h$で展開して2次までとることにする。これは球面を放物面で近似することに対応する。この近似は昔の放物面波のところを思い出して欲しい。
実際に計算してみると \begin{equation} \rho \approx -\frac{\delta}{2z_0(z_0+\delta)}h^2 \nonumber \end{equation} でさらに \begin{equation} \rho \approx -\frac{\delta}{2z_0^2}h^2 \nonumber \end{equation} としていい。デフォーカスの波面は回転対称だから最終的に \begin{equation} \rho_\delta(x,y) \approx -\frac{\delta}{2z_0^2}(x^2+y^2) \end{equation} となる。こいつを式-\ref{defocusedpupil}に代入してFourier変換すればウェスト前後での場が計算できるというわけである。
ただし、Fraunhofer領域なのであまりウェストから遠いところの計算は合わなくなるはずである。どの辺まで正しいのか、というとなかなか難しい。どのみち数値計算を回すことになるので、FFTでエイリアシングが見えたらアウトぐらいの感じだろうか。あまり真面目に考えたことはないけど、収差があると原点から離れたところにも有意な振幅が現れるので、あんがいエイリアシングが起きやすい。
ここではもうめんどくさいので計算例は示さないけど、無収差ガウシアンなら大きなデフォーカスを乗せても計算できるのに、収差(特に非対称な収差)を乗せるとすぐエイリアシングが起こって、細かい振動が計算結果に表れてくる。試してみてください。
ところで、ガウシアンビームの伝播計算を「そんな理想的な計算をしても意味がない」とバカにする人がいる(はっきり言えば前の会社ではそういう意見がメジャーだった)。しかし結像系レンズと違ってN.A.は低いし画角をとることはないので、理想的な計算をしても現実とよく合う、というのが僕の印象である。「全然合わない」という人は磨きのヘボなレンズを使ってるか、アラインメントがヘボなことが多い、と僕は思う。
ずっと昔(十数年前)、大阪郊外のある大学の研究施設を借りて大型定盤の上にレーザのビームを回していたある超有名電気メーカの研究者がいた。ぐるぐると飛ばしてたあげく、必要な場所に絞り込んだスポットの強度分布がぐちゃぐちゃになってて、
「こんなんあかんわ」
と言ってた。彼がほったらかしにしたので僕がそれをじっくり見ると(「続きをやる」と言ってくるかもしれないので、とりあえずいじらないでくれ、と施設の持ち主である先生から言われた。僕はそのレーザの波長で実験できればよかったので、ミラーで取り分けて巨大定盤の隅っこに配置した光学系に取り込んだ)、レーザの出口が定盤から76mmちょっと(この数字でなんのレーザを使っていたかわかるな)を合わせ鏡のクランクで150mmにしてある。そのあと結構しっかりしたスタンドに差し込んだロッドの上にレンズが固定されてて、そういうレンズをいくつか通過するうちに、定盤からの光軸の高さがいつのまにか200mmを超えていて、ロッドの長さギリギリになっている。
「あかんのはあんたのアラインメントやろ」
と密かに思っていたけど、件の人物は装置を投げ出して他所で全然別のことをやり始めた。僕はそのあとのレーザを含めた巨大定盤とそれが設置されているフロアからレンズやメカ部品をそのまま借用できることになった(そのせつは中百舌鳥の先生ありがとうございました)。当時の僕にとっては非常にありがたかったけど、これを読んだ若い光学関係者には、このエピソードから反面教師の存在を学んでいただきたい....
7.2 収差があるときのウェスト付近の場
以前のガウシアンビームの回折でやったように、ウェストでの場の分布はFraunhofer回折として計算できる。つまり、瞳座標を$(x,y)$として瞳での場の大きさを$E$とすると、焦点面での場$\mathcal{E}(\xi,\eta)$は \begin{equation} \mathcal{E}(\xi,\eta) \propto \mathfrak{F}\left\{E(x,y)\right\} \end{equation} となる。ここで$\mathfrak{F}\left\{X\right\}$は場$X$のFourier変換である。ここでのFourier変換は\begin{equation} \mathfrak{F}\left\{X(x,y)\right\} \equiv \int_{-\infty}^\infty \int_{-\infty}^\infty X(x,y) \exp \left(\frac{i k}{z_0} (\xi x+\eta y) \right) dx\, dy \label{fraunhoferagain} \end{equation}
みたいな形で、$z_0$は瞳から焦点面までの距離、いわゆるFocal distanceである。瞳での場は \begin{align} E(x,y) &\equiv A(x,y) \phi(x,y) \nonumber \\ &= A(x,y) \exp 2 \pi i \frac{\tau(x,y)}{\lambda} \end{align} と書ける。ここで$A$は場の大きさで、$\tau$は光路差、すなわち波面収差で、どちらも実の量である。$A$をガウシアンの電場の大きさで$\tau$に収差を仮定してFourier変換すればウェストでの場がわかって、その絶対値の2乗をとれば強度がわかる、というわけである。
しかしこれは一般の収差に関して解析的に計算できないので数値計算する必要がある。
7.3 ウェスト前後での場
Fourier変換することでウェストでの場の様子はわかるけど、その前後はどうなってるのか。それはFraunhofer回折の原理によればデフォーカスの位相$\Phi(x,y)$を瞳に与えればいい、ということになる。つまり$z_0+\delta$の位置での場$\mathcal{E}_\delta(\xi,\eta)$は \begin{align} \mathcal{E}_\delta(\xi,\eta) &\propto \mathfrak{F}\left\{E(x,y)\Phi(x,y)\right\} \nonumber \\ &= \mathfrak{F}\left\{A(x,y) \exp 2 \pi i \frac{\tau(x,y)+\rho_\delta(x,y)}{\lambda}\right\} \label{defocusedpupil} \end{align} となる。ここで$\rho_\delta(x,y)$はデフォーカスに対応する光路差である。$\rho_\delta(x,y)$の具体的な形を計算するために次の図のような、$W$と$W_\delta$の二つの波面を考える。

ある光軸高さ$h \;(\ll R)$での二つの波面の光路差を$\rho$とする。$\rho$が$\delta$でどう表されるかを考える。これは純粋に幾何学の問題なのでまず、 \begin{equation} \rho = \left(R_\delta-\sqrt{R_\delta^2-h^2}\right)-\left(R-\sqrt{R^2-h^2}\right) \end{equation} で、$R_\delta = R+\delta$で$R=z_0$だから \begin{equation} \rho = \left((z_0+\delta)-\sqrt{(z_0+\delta)^2-h^2}\right)-\left(z_0-\sqrt{z_0^2-h^2}\right) \end{equation} となる。これで求まったわけだけど、Fraunhofer回折領域であって、$h \ll z_0$かつ$\delta \ll z_0$としたので$h$で展開して2次までとることにする。これは球面を放物面で近似することに対応する。この近似は昔の放物面波のところを思い出して欲しい。
実際に計算してみると \begin{equation} \rho \approx -\frac{\delta}{2z_0(z_0+\delta)}h^2 \nonumber \end{equation} でさらに \begin{equation} \rho \approx -\frac{\delta}{2z_0^2}h^2 \nonumber \end{equation} としていい。デフォーカスの波面は回転対称だから最終的に \begin{equation} \rho_\delta(x,y) \approx -\frac{\delta}{2z_0^2}(x^2+y^2) \end{equation} となる。こいつを式-\ref{defocusedpupil}に代入してFourier変換すればウェスト前後での場が計算できるというわけである。
ただし、Fraunhofer領域なのであまりウェストから遠いところの計算は合わなくなるはずである。どの辺まで正しいのか、というとなかなか難しい。どのみち数値計算を回すことになるので、FFTでエイリアシングが見えたらアウトぐらいの感じだろうか。あまり真面目に考えたことはないけど、収差があると原点から離れたところにも有意な振幅が現れるので、あんがいエイリアシングが起きやすい。
ここではもうめんどくさいので計算例は示さないけど、無収差ガウシアンなら大きなデフォーカスを乗せても計算できるのに、収差(特に非対称な収差)を乗せるとすぐエイリアシングが起こって、細かい振動が計算結果に表れてくる。試してみてください。
2017-09-23 21:45
nice!(0)
コメント(0)


コメント 0