ガウシアンビームの疑問、続き [ガウシアンビーム]
ガウシアンビームをレンズに通した式は近軸理論のレンズの式と矛盾するのではないかという話の続き。
それぞれの式をもう一度同じ形で書くと \begin{align} d_1 &= \frac{d_0 f}{d_0 - f}&\mbox{（近軸レンズの式）} \nonumber \\ d_1 &= \frac{\displaystyle \left(\frac{\pi w_1^2}{\lambda}\right)^2\frac{1}{f} - d_0\left(1-\frac{d_0}{f} \right)} {\displaystyle\left(\frac{\pi w_1^2}{\lambda}\right)^2 \left(\frac{1}{f} \right)^2 +\left(1-\frac{d_0}{f} \right)^2} &\mbox{（ガウシアンビームでの式）}\nonumber \end{align} ふたつ目のガウシアンビームの式はごちゃごちゃしてるけど前回、近軸波動方程式の解から出発してもこの式にたどり着くことがわかった（Rayleigh長さ$z_R$とレンズの屈折力$\phi$を使うともう少し簡単になる）。
僕は先入観を持ってしまって、ひとつめの近軸のレンズの式の方が正しくて（何と言っても簡単だし）、ガウシアンビームの式の方のどこかに制限があるのではないか、と思い込んでいたんだけど、やっぱり正しいのではないか、と思い直して改めて見直すことにした．．．．
ウェストから$z$の位置でのビーム半径$W(z)$は前回の式-17だった。式-22を使ってレンズに入る前と出た後のビーム半径をプロットすると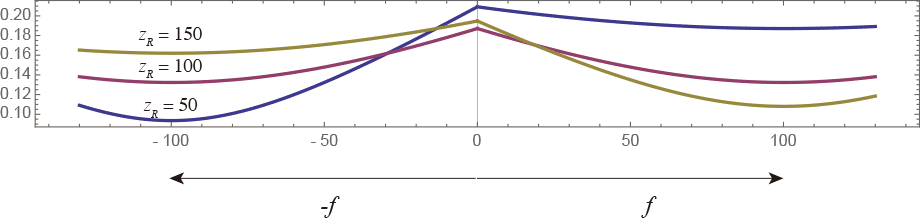
この図では$z=0$の位置に薄肉レンズがあって、物体側のウェスト位置はレンズの焦点位置にあるとしている。レンズの焦点距離は100mm、波長は550nmとして、3つの曲線はRayleigh長さ$z_R$を50mm、100mm、150mmの場合である（50、100、150とか、差が対称じゃなくて比が対称にすればよかったけど、もうめんどくさい）。
$z_R=100$mmのときはレンズの位置がちょうどRayleigh領域の端になっている。この位置での波面の曲率半径$R(z)$は200mmになっていて、レンズによってちょうど対称な形に波面の曲率が変換される。したがって物体側はレンズを対称軸にして折り返した格好になる。
それ以外の$z_R$の場合ではレンズに到達したときの波面の曲率が違うので物体側ではそれにしたがって、曲率半径の大きいとき（$z_R=50$mm）では太く、小さいとき（$z_R=150$mm）では細くなるが、全部$z=100$mmすなわち焦点の位置にウェストがあるのは変わらない。まさしく前回の式-12の言っているとおりである。
もう１つ別の例をプロットしてみる。
この図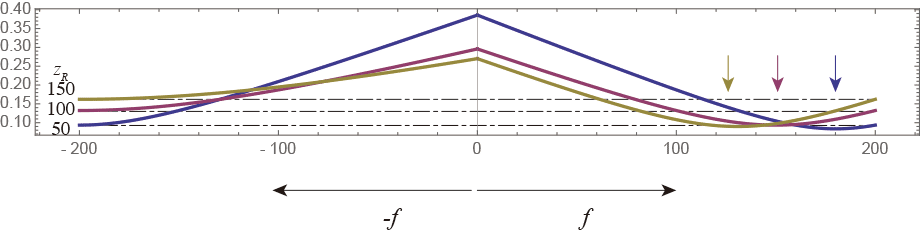
はウェスト位置が前側焦点距離の倍の$z=-200$mmにある場合をプロットした。Rayleigh長さ$z_R$はさっきの3通りである。
こんどはどの場合もレンズ位置での物体側波面の曲率半径は200〜300mmぐらいで、ゆるいので物体側の曲率半径は小さくなって、手前でウェストが現れる。しかしRayleigh長が短くなるにしたがってウェスト位置は遠くなる（矢印で示した）。いずれ$z_R \rightarrow 0$の極限で$z=200$mmの位置、つまり近軸での共役な位置に近づくことが想像できる。
また、$z_R$の値が違えばそれぞれウェスト位置は違うけど、レンズの式で計算したときの共役の位置、つまり焦点距離$f=100$mmのレンズの前後$\pm 200$mmではビーム半径の値は一致している。
Rayleigh長さが一定で、ウェストからレンズまでの距離を変えたとき、つまり下の図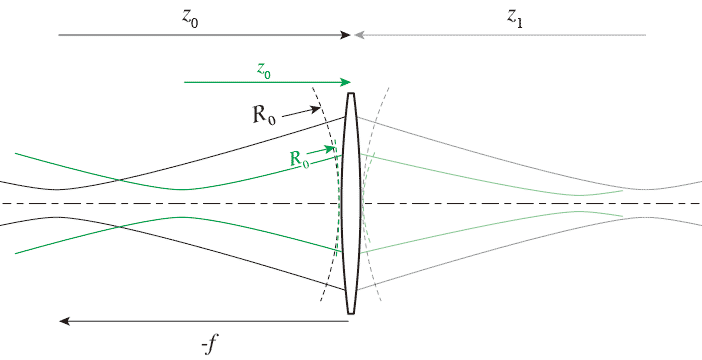
の、黒線の位置から緑線の位置に変えたときどうなるかをみてみる。$z_{R0}$が小さい場合には近軸の幾何光学的計算に近づくので、微妙な場合を計算する。
レンズの焦点距離$f=100$mmで$z_{R0}=100$mmのときをプロットしたのが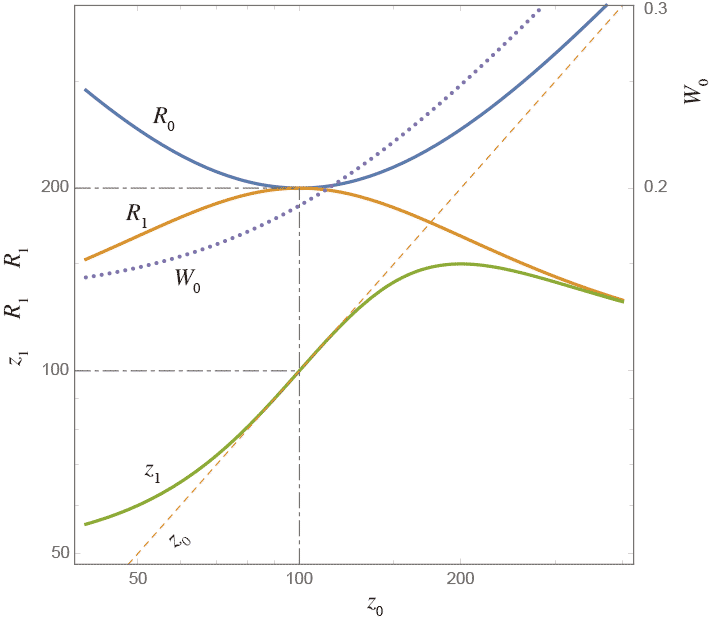
である。
物体側（入射側）の波面の曲率半径$R_0$は$z_0=z_{R0}$のところで最小（曲率最大）になる。レンズによって変換された像側の波面の曲率半径$R_1$はそこで最大になって、それ以外では小さく、すなわち曲率は大きく、レンズにより近いところで焦点を結ぼうとする。
図中赤い細点線が$z_0$で、これは幾何光学的（$z_{R0} \rightarrow 0$)に考えたときの波面の曲率半径に一致する（$z_0$の大きなところで$R_0$と赤点線は漸近する）。$z_0$が小さい領域では$R_0$との乖離が大きくなることがわかる。
一方、レンズ上でのビーム半径$W_0(z_0)$（$=W_1(z_1)$）は物体側のウェストが遠ざかるほど大きくなる（グラフは$\lambda=550$nmの場合）。回折によって、レンズ上でのビーム半径が大きいとより強く絞り込まれるので、$z_0$が大きいところでは像側ウェスト位置はレンズに近づく。
従って、ある物体側ウェスト位置のところでレンズから像側ウェスト位置の最遠ができる。ここはちょうど像側のRayleigh長がレンズの位置、つまり$z_1 = z_{R1}$のはずである。
そして$z_{R0} \ge f$では像側にはかならずウェストができることが直感的にわかる。
ガウシアンビームの波面の曲率半径$R(z)$のふるまいが、こういった幾何光学的な計算とは違う結果を導いていることがわかった。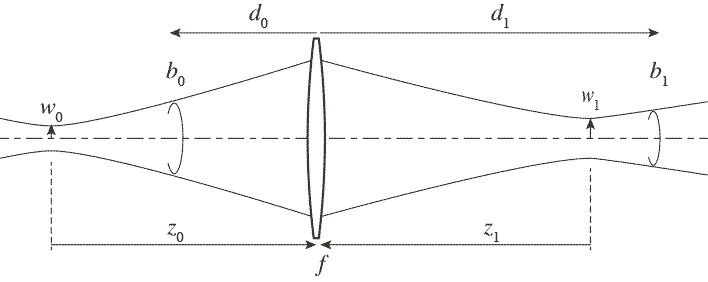
のように、レンズの物体側$z_0$の位置に$w_0$のウェストがあるガウシアンビームがレンズに入射して、物体側の$z_1$の位置に$w_1$のウェストができているとする。それぞれのビームのRayleigh長さを$z_{R0}$と$z_{R1}$とする。
物体側でのレンズから任意の距離$d_0$の位置でのビーム半径$W_0$、$d_1$の位置でのビーム半径$W_1$との比$\beta$は \begin{equation} \beta = \frac{W_1(z_1-d_1)}{W_0(-z_0-d_0)} \end{equation} として、式-22の$z_{R1}$を代入すればいい。
非常に煩わしいけど、Mathematicaにやらせると \begin{equation} \beta = \frac{(d_1+z_0)^2 +z_{R0}^2 -2 \left(z_0(d_1+z_0)+z_{R0}^2 \right)d_1\phi +d_1^2(z_0^2+z_{R0}^2)\phi^2} {(d_0- z_0^2)^2+z_{R0}^2} \label{beta} \end{equation} となる。ほんとかよ。知らんけど。 ここで$d_1$を \begin{equation} d_1 =\frac{d_0}{d_0\phi-1} \end{equation} つまり、近軸の共役の関係としてやると、式-\ref{beta}は簡単になって \begin{equation} \beta = \frac{1}{d_0 \phi -1} \end{equation} となる。これは近軸の倍率の式に等しい。
レンズによりガウシアンビームが変換されたとき、それぞれの領域でのウェスト位置は互いに共役な関係ではない。そもそもレンズによって結像しているわけではなく、言うなれば光線1本をレンズに通した（ひとつの波面が変換された）、という状態に過ぎないので、もともと共役もヘッタクレもないのである。
レンズの物体側焦点位置にウェストがあるとき、像側のウェストはRayleigh長さにかかわらず像側焦点位置にできる。ウェストの大きさの比$\beta_w$は \begin{equation} \beta_w =\frac{1}{z_{R0}\phi} \end{equation} である。ここで$\phi$はレンズの屈折力、${z_{R0}}$は物体側のガウシアンビームのRayleigh長さ \begin{equation} z_{R0}=\frac{\pi w_0^2}{\lambda} \end{equation} である。 これはリレーには便利な特徴である。とくに等倍リレーのためにはRayleigh長さの焦点距離を持つレンズを使えばいい。
一方、共役関係にある位置でのビーム半径$W(z)$は近軸理論に従う、とみなすことができる。ビーム同士がレンズによって結像しているわけではないが、倍率関係は近軸理論で計算したものと一致する。共役もヘッタクレもないはずで、なぜそうなるかは直感的にはピンとこないけど、面白い性質である。
また、Rayleigh長さより短い焦点距離の凸レンズにビームを入射させると、そのレンズをビームのウェストに対してどの距離に置いたとしても必ず像側にはウェストができる。これもカメラレンズのような結像系ばっかりやってるとなんとなく不思議な感じのする性質である。
こういったことはリングジャイロなんかを計算している人には当たり前のことかもしれないけど、僕は全然知らなかった。勉強になったし、結構面白かった。
それと、式の内容に関係なく簡単な式の方に無意識に信頼を寄せてしまうものだということも改めて気がついた。例えば重力方程式$G_{\mu\nu} = \kappa T_{\mu\nu}$（宇宙項がないとして）がベクトルの偏微分方程式だったらうんざりしてたよな（簡単に見えるだけで十分難しいけど）。アインシュタインは偉かったけど、テンソルはまたハミルトンさんなんだよな。カッコいい。
ヘルツ曰く「方程式の方がそれを作ったやつよりも賢い」
自分で作ったわけでもない、人の導いた式を無意識に疑った僕は、そもそもそんな偉そうなことを言える立場じゃなかった。
ところで「ヘッタクレ」って何？
それぞれの式をもう一度同じ形で書くと \begin{align} d_1 &= \frac{d_0 f}{d_0 - f}&\mbox{（近軸レンズの式）} \nonumber \\ d_1 &= \frac{\displaystyle \left(\frac{\pi w_1^2}{\lambda}\right)^2\frac{1}{f} - d_0\left(1-\frac{d_0}{f} \right)} {\displaystyle\left(\frac{\pi w_1^2}{\lambda}\right)^2 \left(\frac{1}{f} \right)^2 +\left(1-\frac{d_0}{f} \right)^2} &\mbox{（ガウシアンビームでの式）}\nonumber \end{align} ふたつ目のガウシアンビームの式はごちゃごちゃしてるけど前回、近軸波動方程式の解から出発してもこの式にたどり着くことがわかった（Rayleigh長さ$z_R$とレンズの屈折力$\phi$を使うともう少し簡単になる）。
僕は先入観を持ってしまって、ひとつめの近軸のレンズの式の方が正しくて（何と言っても簡単だし）、ガウシアンビームの式の方のどこかに制限があるのではないか、と思い込んでいたんだけど、やっぱり正しいのではないか、と思い直して改めて見直すことにした．．．．
4 具体例の計算
4.1 ビーム半径の変化
もう少し直感を養うため、目で見えるようにビーム半径をプロットしてみる。ウェストから$z$の位置でのビーム半径$W(z)$は前回の式-17だった。式-22を使ってレンズに入る前と出た後のビーム半径をプロットすると
$z_R=100$mmのときはレンズの位置がちょうどRayleigh領域の端になっている。この位置での波面の曲率半径$R(z)$は200mmになっていて、レンズによってちょうど対称な形に波面の曲率が変換される。したがって物体側はレンズを対称軸にして折り返した格好になる。
それ以外の$z_R$の場合ではレンズに到達したときの波面の曲率が違うので物体側ではそれにしたがって、曲率半径の大きいとき（$z_R=50$mm）では太く、小さいとき（$z_R=150$mm）では細くなるが、全部$z=100$mmすなわち焦点の位置にウェストがあるのは変わらない。まさしく前回の式-12の言っているとおりである。
もう１つ別の例をプロットしてみる。
この図
こんどはどの場合もレンズ位置での物体側波面の曲率半径は200〜300mmぐらいで、ゆるいので物体側の曲率半径は小さくなって、手前でウェストが現れる。しかしRayleigh長が短くなるにしたがってウェスト位置は遠くなる（矢印で示した）。いずれ$z_R \rightarrow 0$の極限で$z=200$mmの位置、つまり近軸での共役な位置に近づくことが想像できる。
また、$z_R$の値が違えばそれぞれウェスト位置は違うけど、レンズの式で計算したときの共役の位置、つまり焦点距離$f=100$mmのレンズの前後$\pm 200$mmではビーム半径の値は一致している。
4.2 波面の曲率半径との関係
考えてみれば波面の曲率半径$R(z)$は \begin{align} R(z) &= z+\frac{z_R^2}{z} \nonumber \\ \frac{d R(z)}{d z} &= 1-\left(\frac{z_R}{z}\right)^2 \nonumber \end{align} なので、$z=\pm z_R$すなわちRayleigh領域の端でもっとも小さく（曲率がもっとも大きく）なってそれ以外は大きく（曲率は小さく）なる。幾何光学的な、すなわち$z_R \rightarrow 0$の場合では$R(z)=z$なので$z$の小さい（ウェストに近い）とこで違いは大きくなる。Rayleigh長さが一定で、ウェストからレンズまでの距離を変えたとき、つまり下の図
レンズの焦点距離$f=100$mmで$z_{R0}=100$mmのときをプロットしたのが
物体側（入射側）の波面の曲率半径$R_0$は$z_0=z_{R0}$のところで最小（曲率最大）になる。レンズによって変換された像側の波面の曲率半径$R_1$はそこで最大になって、それ以外では小さく、すなわち曲率は大きく、レンズにより近いところで焦点を結ぼうとする。
図中赤い細点線が$z_0$で、これは幾何光学的（$z_{R0} \rightarrow 0$)に考えたときの波面の曲率半径に一致する（$z_0$の大きなところで$R_0$と赤点線は漸近する）。$z_0$が小さい領域では$R_0$との乖離が大きくなることがわかる。
一方、レンズ上でのビーム半径$W_0(z_0)$（$=W_1(z_1)$）は物体側のウェストが遠ざかるほど大きくなる（グラフは$\lambda=550$nmの場合）。回折によって、レンズ上でのビーム半径が大きいとより強く絞り込まれるので、$z_0$が大きいところでは像側ウェスト位置はレンズに近づく。
従って、ある物体側ウェスト位置のところでレンズから像側ウェスト位置の最遠ができる。ここはちょうど像側のRayleigh長がレンズの位置、つまり$z_1 = z_{R1}$のはずである。
そして$z_{R0} \ge f$では像側にはかならずウェストができることが直感的にわかる。
ガウシアンビームの波面の曲率半径$R(z)$のふるまいが、こういった幾何光学的な計算とは違う結果を導いていることがわかった。
4.3 倍率について
任意の位置でのビーム半径の横倍率$\beta$を考えてみる。 この図物体側でのレンズから任意の距離$d_0$の位置でのビーム半径$W_0$、$d_1$の位置でのビーム半径$W_1$との比$\beta$は \begin{equation} \beta = \frac{W_1(z_1-d_1)}{W_0(-z_0-d_0)} \end{equation} として、式-22の$z_{R1}$を代入すればいい。
非常に煩わしいけど、Mathematicaにやらせると \begin{equation} \beta = \frac{(d_1+z_0)^2 +z_{R0}^2 -2 \left(z_0(d_1+z_0)+z_{R0}^2 \right)d_1\phi +d_1^2(z_0^2+z_{R0}^2)\phi^2} {(d_0- z_0^2)^2+z_{R0}^2} \label{beta} \end{equation} となる。ほんとかよ。知らんけど。 ここで$d_1$を \begin{equation} d_1 =\frac{d_0}{d_0\phi-1} \end{equation} つまり、近軸の共役の関係としてやると、式-\ref{beta}は簡単になって \begin{equation} \beta = \frac{1}{d_0 \phi -1} \end{equation} となる。これは近軸の倍率の式に等しい。
5 結論
前回最初の式-2〜3は正しい。なにが間違っていたかというと、ウェストが互いに共役だと思い込んでいたところにある。その誤解のもとは$z_{R0} \rightarrow 0$の場合に物点と像点がちょうどウェスト位置に対応したからである。レンズによりガウシアンビームが変換されたとき、それぞれの領域でのウェスト位置は互いに共役な関係ではない。そもそもレンズによって結像しているわけではなく、言うなれば光線1本をレンズに通した（ひとつの波面が変換された）、という状態に過ぎないので、もともと共役もヘッタクレもないのである。
レンズの物体側焦点位置にウェストがあるとき、像側のウェストはRayleigh長さにかかわらず像側焦点位置にできる。ウェストの大きさの比$\beta_w$は \begin{equation} \beta_w =\frac{1}{z_{R0}\phi} \end{equation} である。ここで$\phi$はレンズの屈折力、${z_{R0}}$は物体側のガウシアンビームのRayleigh長さ \begin{equation} z_{R0}=\frac{\pi w_0^2}{\lambda} \end{equation} である。 これはリレーには便利な特徴である。とくに等倍リレーのためにはRayleigh長さの焦点距離を持つレンズを使えばいい。
一方、共役関係にある位置でのビーム半径$W(z)$は近軸理論に従う、とみなすことができる。ビーム同士がレンズによって結像しているわけではないが、倍率関係は近軸理論で計算したものと一致する。共役もヘッタクレもないはずで、なぜそうなるかは直感的にはピンとこないけど、面白い性質である。
また、Rayleigh長さより短い焦点距離の凸レンズにビームを入射させると、そのレンズをビームのウェストに対してどの距離に置いたとしても必ず像側にはウェストができる。これもカメラレンズのような結像系ばっかりやってるとなんとなく不思議な感じのする性質である。
こういったことはリングジャイロなんかを計算している人には当たり前のことかもしれないけど、僕は全然知らなかった。勉強になったし、結構面白かった。
それと、式の内容に関係なく簡単な式の方に無意識に信頼を寄せてしまうものだということも改めて気がついた。例えば重力方程式$G_{\mu\nu} = \kappa T_{\mu\nu}$（宇宙項がないとして）がベクトルの偏微分方程式だったらうんざりしてたよな（簡単に見えるだけで十分難しいけど）。アインシュタインは偉かったけど、テンソルはまたハミルトンさんなんだよな。カッコいい。
ヘルツ曰く「方程式の方がそれを作ったやつよりも賢い」
自分で作ったわけでもない、人の導いた式を無意識に疑った僕は、そもそもそんな偉そうなことを言える立場じゃなかった。
ところで「ヘッタクレ」って何？
2019-08-12 21:03
nice!(0)
コメント(0)
コメント 0